
【題目】已知函數(shù)f(x)=|x+a|+|x+ ![]() |(a>0)(a<0)
|(a>0)(a<0)
(1)當(dāng)a=2時(shí),求不等式f(x)>3的解集
(2)證明: ![]() .
.
【答案】
(1)解:當(dāng)a=2時(shí),f(x)=|x+2|+|x+ ![]() |,原不等式等價(jià)于
|,原不等式等價(jià)于 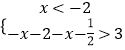
或 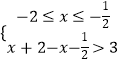 或
或 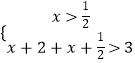
解得:x<﹣ ![]() 或x∈或
或x∈或 ![]() ,所以不等式的解集為{x|x<﹣
,所以不等式的解集為{x|x<﹣ ![]() 或
或 ![]()
(2)解:f(m)+f(﹣ ![]() )=|m+a|+|m+
)=|m+a|+|m+ ![]() |+|﹣
|+|﹣ ![]() +a|+|﹣
+a|+|﹣ ![]() +
+ ![]() |
|
= ![]()
【解析】(1)分類討論,解不等式,即可得出結(jié)論;(2)f(m)+f(﹣ ![]() )=|m+a|+|m+
)=|m+a|+|m+ ![]() |+|﹣
|+|﹣ ![]() +a|+|﹣
+a|+|﹣ ![]() +
+ ![]() |,利用三角不等式,及基本不等式即可證明結(jié)論.
|,利用三角不等式,及基本不等式即可證明結(jié)論.
【考點(diǎn)精析】解答此題的關(guān)鍵在于理解絕對值不等式的解法的相關(guān)知識,掌握含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規(guī)律:關(guān)鍵是去掉絕對值的符號,以及對不等式的證明的理解,了解不等式證明的幾種常用方法:常用方法有:比較法(作差,作商法)、綜合法、分析法;其它方法有:換元法、反證法、放縮法、構(gòu)造法,函數(shù)單調(diào)性法,數(shù)學(xué)歸納法等.


 名校提分一卷通系列答案
名校提分一卷通系列答案 課程達(dá)標(biāo)測試卷闖關(guān)100分系列答案
課程達(dá)標(biāo)測試卷闖關(guān)100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關(guān)100分系列答案
全能闖關(guān)100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知單調(diào)遞增的等比數(shù)列![]() 滿足
滿足![]() ,且
,且![]() 是
是![]() 的等差中項(xiàng).
的等差中項(xiàng).
(Ⅰ)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)若![]() ,對任意正數(shù)數(shù)
,對任意正數(shù)數(shù)![]() ,
, ![]() 恒成立,試求
恒成立,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)雙曲線 ![]() (a>0,b>0)的左焦點(diǎn)為F1 , 左頂點(diǎn)為A,過F1作x軸的垂線交雙曲線于P、Q兩點(diǎn),過P作PM垂直QA于M,過Q作QN垂直PA于N,設(shè)PM與QN的交點(diǎn)為B,若B到直線PQ的距離大于a+
(a>0,b>0)的左焦點(diǎn)為F1 , 左頂點(diǎn)為A,過F1作x軸的垂線交雙曲線于P、Q兩點(diǎn),過P作PM垂直QA于M,過Q作QN垂直PA于N,設(shè)PM與QN的交點(diǎn)為B,若B到直線PQ的距離大于a+ ![]() ,則該雙曲線的離心率取值范圍是( )
,則該雙曲線的離心率取值范圍是( )
A.(1﹣ ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2 ![]() )
)
D.(2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,F(xiàn)1、F2分別是橢圓的左、右焦點(diǎn),M為橢圓上除長軸端點(diǎn)外的任意一點(diǎn),且△MF1F2的周長為4+2
,F(xiàn)1、F2分別是橢圓的左、右焦點(diǎn),M為橢圓上除長軸端點(diǎn)外的任意一點(diǎn),且△MF1F2的周長為4+2 ![]() .
.
(1)求橢圓C的方程;
(2)過點(diǎn)D(0,﹣2)作直線l與橢圓C交于A、B兩點(diǎn),點(diǎn)N滿足 ![]() (O為原點(diǎn)),求四邊形OANB面積的最大值,并求此時(shí)直線l的方程.
(O為原點(diǎn)),求四邊形OANB面積的最大值,并求此時(shí)直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè) ![]() 是定義在
是定義在 ![]() 上的奇函數(shù),且對任意實(shí)數(shù)
上的奇函數(shù),且對任意實(shí)數(shù) ![]() ,恒有
,恒有 ![]() .當(dāng)
.當(dāng) ![]() 時(shí),
時(shí), ![]() .
.
(1)求證: ![]() 是周期函數(shù);
是周期函數(shù);
(2)當(dāng) ![]() 時(shí),求
時(shí),求 ![]() 的解析式;
的解析式;
(3)計(jì)算 ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f (x)=Asin(ωx+φ),(0<φ<π)的圖象如圖所示,若f (x0)=3,x0∈( ![]() ,
, ![]() ),則sinx0的值為( )
),則sinx0的值為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
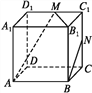
【題目】如圖所示,在正方體ABCD-A1B1C1D1中,M,N分別為棱C1D1,C1C的中點(diǎn),有以下四個(gè)結(jié)論:
①直線AM與CC1是相交直線;②直線AM與BN是平行直線;
③直線BN與MB1是異面直線; ④直線MN與AC所成的角為60°.
其中正確的結(jié)論為___ (注:把你認(rèn)為正確的結(jié)論序號都填上).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐 ![]() 中,
中, ![]() 底面
底面 ![]() ,底面
,底面 ![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為 ![]() 的中點(diǎn),平面
的中點(diǎn),平面 ![]() 交
交 ![]() 于
于 ![]() 點(diǎn).、
點(diǎn).、
(1)求證: ![]() ;
;
(2)求二面角 ![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ![]() .
.
(1)當(dāng) ![]() 時(shí),求
時(shí),求 ![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)設(shè) ![]() ,
, ![]() 是曲線
是曲線 ![]() 圖象上的兩個(gè)相異的點(diǎn),若直線
圖象上的兩個(gè)相異的點(diǎn),若直線 ![]() 的斜率
的斜率 ![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù) ![]() 的取值范圍;
的取值范圍;
(3)設(shè)函數(shù) ![]() 有兩個(gè)極值點(diǎn)
有兩個(gè)極值點(diǎn) ![]() ,
, ![]() ,且
,且 ![]() ,若
,若 ![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù) ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com