
【題目】已知函數![]() ,其圖象的一條切線為
,其圖象的一條切線為![]() .
.
(1)求實數![]() 的值;
的值;
(2)求證:若![]() ,則
,則![]() .
.
【答案】(1)![]() ;(2)答案見解析
;(2)答案見解析
【解析】
(1)假設切點,根據曲線在某點處導數的幾何意義,以及已知的切線方程,可得![]() ,然后研究
,然后研究![]() 可得
可得![]() ,最后代值計算,可得結果.
,最后代值計算,可得結果.
(2)構建函數![]() ,計算
,計算![]() ,并利用二階導判斷
,并利用二階導判斷![]() 的單調性,根據
的單調性,根據![]() 的值域來判斷
的值域來判斷![]() 的單調性,進一步求得
的單調性,進一步求得![]() ,可得結果.
,可得結果.
(1)函數定義域為![]()
∵![]() ,∴
,∴![]() .
.
由題可知:
![]() 在點
在點![]() 處的切線為
處的切線為![]() ,
,
則![]() 且
且![]() ,
,
∴![]() ,即
,即![]() .
.
令![]() ,
,
則![]() .
.
當![]() 時,
時,
![]() ,
,![]() 在
在![]() 單調遞增;
單調遞增;
當![]() 時,
時,
![]() ,
,![]() 在
在![]() 單調遞減.
單調遞減.
當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() .
.
∴![]() ,
,![]() .故實數
.故實數![]() 的值為
的值為![]() .
.
(2)令![]()
即![]()
則![]() .
.
即![]()
令![]() ,
,
則![]() ,
,
∵![]() 恒成立,
恒成立,
∴![]() 在
在![]() 單調遞減,即
單調遞減,即![]() 在
在![]() 單調遞減.
單調遞減.
又![]() ,
,
![]() ,
,
∴![]() ,使得
,使得![]() .
.
∴當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ,
,
故![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減.
單調遞減.
∴![]() .
.
又![]() ,即
,即![]() ,
,
∴![]() ,
,
![]()
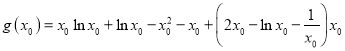
![]() .
.
令![]() ,
,![]() .
.
則![]() .
.
∵![]() 恒成立,
恒成立,
∴![]() ,故
,故![]() 在
在![]() 單調遞增.
單調遞增.
∴![]() ,
,
故![]() ,
,
即![]() .
.
∴當![]() 時,
時,![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 的焦點為F,準線為l,過準線l上一點
的焦點為F,準線為l,過準線l上一點![]() 且斜率為k的直線
且斜率為k的直線![]() 交拋物線C于A,B兩點,線段AB的中點為P,直線PF交拋物線C于D,E兩點.
交拋物線C于A,B兩點,線段AB的中點為P,直線PF交拋物線C于D,E兩點.
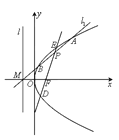
(1)求拋物線C的方程及k的取值范圍;
(2)是否存在k值,使點P是線段DE的中點?若存在,求出k值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的圖象為C,如下結論中正確的是( )
的圖象為C,如下結論中正確的是( )
①圖象C關于直線![]() 對稱;②函數
對稱;②函數![]() 在區間
在區間![]() 內是增函數;
內是增函數;
③圖象C關于點![]() 對稱;④由
對稱;④由![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度可以得到圖象C
個單位長度可以得到圖象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個統計案例如下:
①為了探究患慢性支氣管炎與吸煙關系,調查了339名50歲以上的人,調查結果如表:
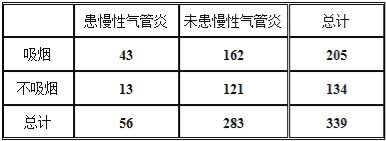
②為了解某地母親與女兒身高的關系,隨機測得10對母女的身高如下表: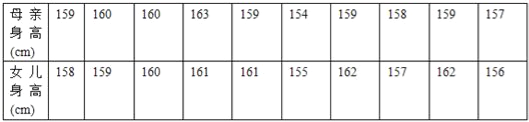
則對這些數據的處理所應用的統計方法是( )
A.①回歸分析②取平均值
B.①獨立性檢驗②回歸分析
C.①回歸分析②獨立性檢驗
D.①獨立性檢驗②取平均值
查看答案和解析>>
科目:高中數學 來源: 題型:
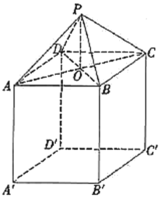
【題目】如圖所示,一個倉庫設計由上部屋頂和下部主體兩部分組成,屋頂的形狀是四棱錐![]() ,四邊形
,四邊形![]() 是正方形,點
是正方形,點![]() 為正方形
為正方形![]() 的中心,
的中心,![]() 平面
平面![]() ;下部的形狀是長方體
;下部的形狀是長方體![]() .已知上部屋頂造價與屋頂面積成正比,比例系數為
.已知上部屋頂造價與屋頂面積成正比,比例系數為![]() ,下部主體造價與高度成正比,比例系數為
,下部主體造價與高度成正比,比例系數為![]() .若欲造一個上、下總高度為10
.若欲造一個上、下總高度為10![]() ,
,![]()
![]() 的倉庫,則當總造價最低時,
的倉庫,則當總造價最低時,![]() ( )
( )
A.![]()
![]() B.
B.![]()
![]() C.4
C.4![]() D.
D.![]()
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保障人民群眾的身體健康,在預防新型冠狀病毒期間,貴陽市市場監督管理局加強了對市場的監管力度,對生產口罩的某工廠利用隨機數表對生產的![]() 個口罩進行抽樣測試是否合格,先將
個口罩進行抽樣測試是否合格,先將![]() 個口罩進行編號,編號分別為
個口罩進行編號,編號分別為![]() ;從中抽取
;從中抽取![]() 個樣本,如下提供隨機數表的第
個樣本,如下提供隨機數表的第![]() 行到第
行到第![]() 行:
行:
![]()
![]()
![]()
若從表中第![]() 行第
行第![]() 列開始向右依次讀取
列開始向右依次讀取![]() 個數據,則得到的第
個數據,則得到的第![]() 個樣本編號為( )
個樣本編號為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設三角形的邊長為不相等的整數,且最大邊長為n,這些三角形的個數為an.
(1)求數列{an}的通項公式;
(2)在1,2,…,100中任取三個不同的整數,求它們可以是一個三角形的三條邊長的概率.
附:1+22+32+…+n2![]() ;1+23+33+…+n3
;1+23+33+…+n3![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為常數,且
為常數,且![]() .
.
(1)若![]() 是奇函數,求
是奇函數,求![]() 的取值集合
的取值集合![]() ;
;
(2)當![]() 時,設
時,設![]() 的反函數
的反函數![]() ,且
,且![]() 的圖象與
的圖象與![]() 的圖象關于
的圖象關于![]() 對稱,求
對稱,求![]() 的取值集合
的取值集合![]() ;
;
(3)對于問題(1)(2)中的![]() 、
、![]() ,當
,當![]() 時,不等式
時,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com