
【題目】如圖,已知三棱柱![]() 的所有棱長都相等,且側棱垂直于底面,由
的所有棱長都相等,且側棱垂直于底面,由![]() 沿棱柱側面經過棱
沿棱柱側面經過棱![]() 到點
到點![]() 的最短路線長為
的最短路線長為![]() ,設這條最短路線與
,設這條最短路線與![]() 的交點為
的交點為![]() .
.

(1)求三棱柱![]() 的體積;
的體積;
(2)證明:平面![]() 平面
平面![]() .
.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某廠商為了解用戶對其產品是否滿意,在使用產品的用戶中隨機調查了80人,結果如下表:
(1)根據上述,現用分層抽樣的方法抽取對產品滿意的用戶5人,在這5人中任選2人,求被選中的恰好是男、女用戶各1人的概率;
(2)有多大把握認為用戶對該產品是否滿意與用戶性別有關?請說明理由.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱柱![]() 的所有棱長都相等,且側棱垂直于底面,由
的所有棱長都相等,且側棱垂直于底面,由![]() 沿棱柱側面經過棱
沿棱柱側面經過棱![]() 到點
到點![]() 的最短路線長為
的最短路線長為![]() ,設這條最短路線與
,設這條最短路線與![]() 的交點為
的交點為![]() .
.
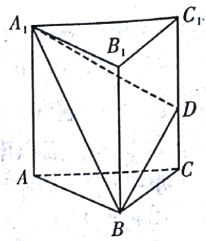
(1)求三棱柱![]() 的體積;
的體積;
(2)證明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設U=R,A={x|x≤2,或x≥5},B= ![]() ,C={x|a<x<a+1}
,C={x|a<x<a+1}
(1)求A∪B和(UA)∩B
(2)若B∩C=C,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,且
,且![]() ).
).
(1)當![]() 時,設集合
時,設集合![]() ,求集合
,求集合![]() ;
;
(2)在(1)的條件下,若![]() ,且滿足
,且滿足![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(3)若對任意的![]() ,存在
,存在![]() ,使不等式
,使不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象過點
的圖象過點![]() ,且與
,且與![]() 軸有唯一的交點
軸有唯一的交點![]() .
.
(1)求![]() 的表達式;
的表達式;
(2)設函數![]() ,若
,若![]() 上是單調函數,求實數
上是單調函數,求實數![]() 的取值范圍;
的取值范圍;
(3)設函數![]() ,記此函數的最小值為
,記此函數的最小值為![]() ,求
,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】銳角△ABC中,角A、B、C所對的邊分別為a、b、c,且tanA﹣tanB= ![]() (1+tanAtanB). (Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(1+tanAtanB). (Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(Ⅱ)已知向量 ![]() =(sinA,cosA),
=(sinA,cosA), ![]() =(cosB,sinB),求|3
=(cosB,sinB),求|3 ![]() ﹣2
﹣2 ![]() |的取值范圍.
|的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】綜合題。
(1)已知f( ![]() +1)=x+2
+1)=x+2 ![]() ,求f(x)的解析式;
,求f(x)的解析式;
(2)已知f(x)是一次函數,且滿足3f(x+1)﹣2f(x﹣1)=2x+17,求f(x)的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com