
【題目】銳角△ABC中,角A、B、C所對的邊分別為a、b、c,且tanA﹣tanB= ![]() (1+tanAtanB). (Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(1+tanAtanB). (Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(Ⅱ)已知向量 ![]() =(sinA,cosA),
=(sinA,cosA), ![]() =(cosB,sinB),求|3
=(cosB,sinB),求|3 ![]() ﹣2
﹣2 ![]() |的取值范圍.
|的取值范圍.
【答案】解:(I)∵tanA﹣tanB= ![]() (1+tanAtanB),
(1+tanAtanB),
∴tan(A﹣B)= ![]() =
= ![]() ,
,
∵A,B是銳角,∴A﹣B= ![]() .
.
∵c2=a2+b2﹣ab,∴ ![]() =
= ![]() =
= ![]() ,
,
∵C為銳角,∴ ![]() .
.
∴ ![]() ,解得A=
,解得A= ![]() ,B=
,B= ![]() .
.
(II)∵向量 ![]() =(sinA,cosA),
=(sinA,cosA), ![]() =(cosB,sinB),
=(cosB,sinB),
∴ ![]() =1,
=1, ![]() =sinAcosB+cosAsinB=sin(A+B)=
=sinAcosB+cosAsinB=sin(A+B)= ![]() ,
,
∵銳角△ABC,∴ ![]() ,A+B=
,A+B= ![]() ,
,
解得 ![]() .∴
.∴ ![]() ,
,
∴ ![]() ∈
∈ ![]() .
.
∵|3 ![]() ﹣2
﹣2 ![]() |=
|= ![]() =
=  ,
,
∴ ![]() <7.
<7.
∴  ∈
∈ ![]() ,
,
∴|3 ![]() ﹣2
﹣2 ![]() |∈
|∈ ![]()
【解析】(I)利用兩角差的正切公式和余弦定理及其三角形的內角和定理即可得出;(II)利用數量積運算及其性質、銳角三角形的定義、正弦函數的單調性即可得出.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)(sinx+cosx)2+2cos2x﹣2
(1)求函數f(x)的最小正周期T;
(2)求f(x)的最大值,并指出取得最大值時x取值集合;
(3)當x∈[ ![]() ,
, ![]() ]時,求函數f(x)的值域.
]時,求函數f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知三棱柱![]() 的所有棱長都相等,且側棱垂直于底面,由
的所有棱長都相等,且側棱垂直于底面,由![]() 沿棱柱側面經過棱
沿棱柱側面經過棱![]() 到點
到點![]() 的最短路線長為
的最短路線長為![]() ,設這條最短路線與
,設這條最短路線與![]() 的交點為
的交點為![]() .
.

(1)求三棱柱![]() 的體積;
的體積;
(2)證明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分別為A1C1、B1C1的中點,D為棱CC1上任一點. 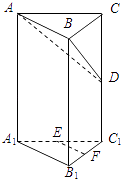
(Ⅰ)求證:直線EF∥平面ABD;
(Ⅱ)求證:平面ABD⊥平面BCC1B1 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=lnx﹣ax,a∈R.
(1)當x=1時,函數f(x)取得極值,求a的值;
(2)當0<a< ![]() 時,求函數f(x)在區間[1,2]上的最大值;
時,求函數f(x)在區間[1,2]上的最大值;
(3)當a=﹣1時,關于x的方程2mf(x)=x2(m>0)有唯一實數解,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇函數,
為奇函數, ![]() 為常數.
為常數.
(1)確定![]() 的值;
的值;
(2)求證: ![]() 是
是![]() 上的增函數;
上的增函數;
(3)若對于區間![]() 上的每一個
上的每一個![]() 值,不等式
值,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一種新型的洗衣液,去污速度特別快.已知每投放![]() (
(![]() 且
且![]() )個單位的洗衣液在一定量水的洗衣機中,它在水中釋放的濃度
)個單位的洗衣液在一定量水的洗衣機中,它在水中釋放的濃度![]() (克/升)隨著時間
(克/升)隨著時間![]() (分鐘) 變化的函數關系式近似為
(分鐘) 變化的函數關系式近似為![]() ,其中
,其中 .根據經驗,當水中洗衣液的濃度不低于4(克/升)時,它才能起到有效去污的作用.
.根據經驗,當水中洗衣液的濃度不低于4(克/升)時,它才能起到有效去污的作用.
(1)若投放![]() 個單位的洗衣液,3分鐘時水中洗衣液的濃度為4 (克/升),求
個單位的洗衣液,3分鐘時水中洗衣液的濃度為4 (克/升),求![]() 的值;
的值;
(2)若投放4個單位的洗衣液,則有效去污時間可達幾分鐘?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E的右焦點與拋物線y2=4x的焦點重合,點M ![]() 在橢圓E上. (Ⅰ)求橢圓E的標準方程;
在橢圓E上. (Ⅰ)求橢圓E的標準方程;
(Ⅱ)設P(﹣4,0),直線y=kx+1與橢圓E交于A,B兩點,若直線PA,PB關于x軸對稱,求k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com