
【題目】現(xiàn)有流量均為![]() 的兩條河流
的兩條河流![]() 匯合于某處后,不斷混合,它們的含沙量分別為
匯合于某處后,不斷混合,它們的含沙量分別為![]() 和
和![]() .假設(shè)從匯合處開(kāi)始,沿岸設(shè)有若干個(gè)觀測(cè)點(diǎn),兩股水流在流往相鄰兩個(gè)觀測(cè)點(diǎn)的過(guò)程中,其混合效果相當(dāng)于兩股水流在1秒內(nèi)交換
.假設(shè)從匯合處開(kāi)始,沿岸設(shè)有若干個(gè)觀測(cè)點(diǎn),兩股水流在流往相鄰兩個(gè)觀測(cè)點(diǎn)的過(guò)程中,其混合效果相當(dāng)于兩股水流在1秒內(nèi)交換![]() 的水量,其交換過(guò)程為從A股流入B股
的水量,其交換過(guò)程為從A股流入B股![]() 的水量,經(jīng)混合后,又從B股流入A股
的水量,經(jīng)混合后,又從B股流入A股![]() 水并混合,問(wèn)從第幾個(gè)觀測(cè)點(diǎn)開(kāi)始,兩股河水的含沙量之差小于
水并混合,問(wèn)從第幾個(gè)觀測(cè)點(diǎn)開(kāi)始,兩股河水的含沙量之差小于![]() .(不考慮泥沙沉淀).
.(不考慮泥沙沉淀).
【答案】第9個(gè)
【解析】
設(shè)第n個(gè)觀測(cè)點(diǎn)A股水流含沙量為![]() ,B股水流含沙量為bn.由已知我們易得
,B股水流含沙量為bn.由已知我們易得![]() 是以
是以![]() 為首項(xiàng),
為首項(xiàng),![]() 為公比的等比數(shù)列.求出數(shù)列的通項(xiàng)公式后,構(gòu)造不等式,解不不等式,即可得到結(jié)論.
為公比的等比數(shù)列.求出數(shù)列的通項(xiàng)公式后,構(gòu)造不等式,解不不等式,即可得到結(jié)論.
解:設(shè)第n個(gè)觀測(cè)點(diǎn)A股水流含沙量為![]() ,B股水流含沙量為
,B股水流含沙量為![]() .
.
![]()
即:![]()
![]() 是以
是以![]() 為首項(xiàng),
為首項(xiàng),![]() 為公比的等比數(shù)列.
為公比的等比數(shù)列.
![]()
解不等式![]()
得![]() ,又由n正整數(shù),
,又由n正整數(shù),
![]()
因此,從第9個(gè)觀測(cè)點(diǎn)開(kāi)始,兩股水流含沙量之差小于0.01kg/m3.


 全能測(cè)控期末小狀元系列答案
全能測(cè)控期末小狀元系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,由半圓![]() 和部分拋物線
和部分拋物線![]() 合成的曲線
合成的曲線![]() 稱為“羽毛球開(kāi)線”,曲線
稱為“羽毛球開(kāi)線”,曲線![]() 與
與![]() 軸有
軸有![]() 兩個(gè)焦點(diǎn),且經(jīng)過(guò)點(diǎn)
兩個(gè)焦點(diǎn),且經(jīng)過(guò)點(diǎn)![]()

(1)求![]() 的值;
的值;
(2)設(shè)![]()
![]() 為曲線
為曲線![]() 上的動(dòng)點(diǎn),求
上的動(dòng)點(diǎn),求![]() 的最小值;
的最小值;
(3)過(guò)![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與“羽毛球形線”相交于點(diǎn)
與“羽毛球形線”相交于點(diǎn)![]() 三點(diǎn),問(wèn)是否存在實(shí)數(shù)
三點(diǎn),問(wèn)是否存在實(shí)數(shù)![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請(qǐng)說(shuō)明理由。
的值;若不存在,請(qǐng)說(shuō)明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)于函數(shù)![]() 定義
定義![]() 已知偶函數(shù)
已知偶函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() 當(dāng)
當(dāng)![]() 且
且![]() 時(shí),
時(shí),![]()
(1)求![]() 并求出函數(shù)
并求出函數(shù)![]() 的解析式;
的解析式;
(2)若存在實(shí)數(shù)![]() 使得函數(shù)
使得函數(shù)![]() 在
在![]() 上的值域?yàn)?/span>
上的值域?yàn)?/span>![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列判斷正確的是( )
A.若隨機(jī)變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,
,![]() ,則
,則![]() ;
;
B.已知直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ,則“
,則“![]() ”是“
”是“![]() ”的充分不必要條件;
”的充分不必要條件;
C.若隨機(jī)變量![]() 服從二項(xiàng)分布:
服從二項(xiàng)分布:![]() ,則
,則![]() ;
;
D.![]() 是
是![]() 的充分不必要條件.
的充分不必要條件.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),對(duì)于一切
時(shí),對(duì)于一切![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 內(nèi)總存在唯一零點(diǎn),求
內(nèi)總存在唯一零點(diǎn),求![]() 的取值范圍;
的取值范圍;
(2)若![]() 區(qū)間
區(qū)間![]() 上是單調(diào)函數(shù),求
上是單調(diào)函數(shù),求![]() 的取值范圍;
的取值范圍;
(3)當(dāng)![]() ,
,![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 在區(qū)間
在區(qū)間![]() 內(nèi)的零點(diǎn)為
內(nèi)的零點(diǎn)為![]() ,判斷數(shù)列
,判斷數(shù)列![]() ,
,![]() ,…,
,…,![]() ,…的增減性,并說(shuō)明理由.
,…的增減性,并說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,若同時(shí)滿足以下條件:
,若同時(shí)滿足以下條件:
①![]() 在D上單調(diào)遞減或單調(diào)遞增;
在D上單調(diào)遞減或單調(diào)遞增;
②存在區(qū)間![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,那么稱
,那么稱![]() 為閉函數(shù).
為閉函數(shù).
(1)求閉函數(shù)![]() 符合條件②的區(qū)間
符合條件②的區(qū)間![]() ;
;
(2)判斷函數(shù)![]() 是不是閉函數(shù)?若是請(qǐng)找出區(qū)間
是不是閉函數(shù)?若是請(qǐng)找出區(qū)間![]() ;若不是請(qǐng)說(shuō)明理由;
;若不是請(qǐng)說(shuō)明理由;
(3)若![]() 是閉函數(shù),求實(shí)數(shù)
是閉函數(shù),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】斜三棱柱![]() 中,底面是邊長(zhǎng)為
中,底面是邊長(zhǎng)為![]() 的正三角形,側(cè)棱長(zhǎng)為
的正三角形,側(cè)棱長(zhǎng)為![]() ,側(cè)棱
,側(cè)棱![]() 與底面相鄰兩邊
與底面相鄰兩邊![]()
![]() 都成
都成![]() 角,求此三棱柱的側(cè)面積和體積.
角,求此三棱柱的側(cè)面積和體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]()
![]() .
.
(1)當(dāng)![]() 時(shí),討論
時(shí),討論![]() 的單調(diào)性;
的單調(diào)性;
(2)設(shè)![]() ,當(dāng)
,當(dāng)![]() 時(shí),若對(duì)任意
時(shí),若對(duì)任意![]() ,存在
,存在![]() 使
使![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 取值.
取值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
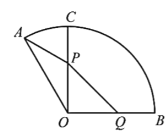
【題目】如圖是一個(gè)半徑為1千米的扇形景點(diǎn)的平面示意圖,![]() .原有觀光道路OC,且
.原有觀光道路OC,且![]() .為便于游客觀賞,景點(diǎn)管理部門(mén)決定新建兩條道路PQ、PA,其中P在原道路OC(不含端點(diǎn)O、C)上,Q在景點(diǎn)邊界OB上,且
.為便于游客觀賞,景點(diǎn)管理部門(mén)決定新建兩條道路PQ、PA,其中P在原道路OC(不含端點(diǎn)O、C)上,Q在景點(diǎn)邊界OB上,且![]() ,同時(shí)維修原道路的OP段,因地形原因,新建PQ段、PA段的每千米費(fèi)用分別是
,同時(shí)維修原道路的OP段,因地形原因,新建PQ段、PA段的每千米費(fèi)用分別是![]() 萬(wàn)元、
萬(wàn)元、![]() 萬(wàn)元,維修OP段的每千米費(fèi)用是
萬(wàn)元,維修OP段的每千米費(fèi)用是![]() 萬(wàn)元.
萬(wàn)元.
(1)設(shè)![]() ,求所需總費(fèi)用
,求所需總費(fèi)用![]() ,并給出
,并給出![]() 的取值范圍;
的取值范圍;
(2)當(dāng)P距離O處多遠(yuǎn)時(shí),總費(fèi)用最小.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com