【題目】下列判斷正確的是（ ）
A.若隨機變量
服從正態(tài)分布
，
，則
；
B.已知直線
平面
，直線
平面
，則“
”是“
”的必要不充分條件；
C.若隨機變量服從二項分布：
，則
；
D.已知直線
經(jīng)過點
，則
的取值范圍是
53隨堂測系列答案科目：高中數(shù)學 來源： 題型：
【題目】為了了解某市高中學生的漢字書寫水平，在全市范圍內(nèi)隨機抽取了近千名學生參加漢字聽寫考試，將所得數(shù)據(jù)進行分組，分組區(qū)間為：
，并繪制出頻率分布直方圖，如圖所示.
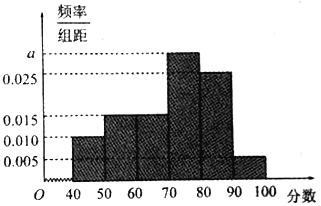
（1）求頻率分布直方圖中
的值，并估計該市高中學生的平均成績；
（2）設
、
、
、
四名學生的考試成績在區(qū)間
內(nèi)，
、
兩名學生的考試成績在區(qū)間
內(nèi)，現(xiàn)從這6名學生中任選兩人參加座談會，求學生、至少有一人被選中的概率.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知在直角三角形ABC中，
，
（如右圖所示）
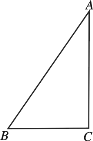
（Ⅰ）若以AC為軸，直角三角形ABC旋轉(zhuǎn)一周，試說明所得幾何體的結(jié)構(gòu)特征并求所得幾何體的表面積.
（Ⅱ）一只螞蟻在問題（Ⅰ）形成的幾何體上從點B繞著幾何體的側(cè)面爬行一周回到點B，求螞蟻爬行的最短距離.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知三棱錐M-ABC中，MA=MB=MC=AC=
，AB=BC=2，O為AC的中點，點N在邊BC上，且
.
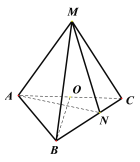
（1）證明：BO
平面AMC；
（2）求二面角N-AM-C的正弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知定義在
上的函數(shù)
的圖像關(guān)于直線
對稱，且當
時，
，過點
作曲線
的兩條切線,若這兩條切線互相垂直,則該函數(shù)的最小值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在四棱錐P－ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP＝AB＝AD＝1．
（Ⅰ）若直線PB與CD所成角的大小為
，求BC的長；
（Ⅱ）求二面角B－PD－A的余弦值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)
，
.
（1）當
（
為自然對數(shù)的底數(shù)）時，求
的極小值；
（2）討論函數(shù)
零點的個數(shù).
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】交強險是車主必須為機動車購買的險種，若普通6座以下私家車投保交強險第一年的費用 (基準保費)統(tǒng)一為
元，在下一年續(xù)保時，實行的是費率浮動機制，保費是與上一年度車輛發(fā)生道路交通安全違法行為或者道路交通事故的情況相聯(lián)系的.交強險第二年價格計算公式具體如下:交強險最終保費
基準保費
（
浮動比率
).發(fā)生交通事故的次數(shù)越多，出險次數(shù)的就越多，費率也就越髙，具體浮動情況如下表：
某機構(gòu)為了研究某一品牌普通6座以下私家車的投保情況，為此搜集并整理了100輛這一品牌普通6座以下私家車一年內(nèi)的出險次數(shù)，得到下面的柱狀圖：
已知小明家里有一輛該品牌普通6座以下私家車且需要續(xù)保，續(xù)保費用為
元.
（1）記
為事件“
”，求
的估計值；
（2）求
的平均估計值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知
的三邊長為a，b，c，有下列四個命題：
①以
，
，
為邊長的三角形一定存在；
②以
，
，
為邊長的三角形一定存在；
③以
，
，
為邊長的三角形一定存在；
④以
，
，
為邊長的三角形一定存在．
其中正確的是（ ）
A.①③B.②③C.②④D.①④
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
