
【題目】設(shè)函數(shù)f(x)=|3x﹣1|+ax+3
(1)若a=1,解不等式f(x)≤4;
(2)若函數(shù)f(x)有最小值,求a的取值范圍.
【答案】
(1)解:當(dāng)a=1時,f(x)=|3x﹣1|+x+3,
當(dāng)x ![]() 時,f(x)≤4可化為3x﹣1+x+3≤4,解得
時,f(x)≤4可化為3x﹣1+x+3≤4,解得 ![]() ;
;
當(dāng)x ![]() 時,f(x)≤4可化為﹣3x+1+x+3≤4,解得
時,f(x)≤4可化為﹣3x+1+x+3≤4,解得 ![]() .
.
綜上可得,原不等式的解集為{x| ![]() },
},
(2)解:f(x)=|3x﹣1|+ax+3= 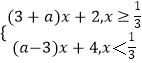
函數(shù)f(x)有最小值的充要條件為 ![]() ,
,
即﹣3≤a≤3
【解析】(1)需要去掉絕對值,得到不等式解得即可,(2)把含所有絕對值的函數(shù),化為分段函數(shù),再根據(jù)函數(shù)f(x)有最小值的充要條件,即可求得.
【考點精析】本題主要考查了絕對值不等式的解法的相關(guān)知識點,需要掌握含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規(guī)律:關(guān)鍵是去掉絕對值的符號才能正確解答此題.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C過點![]() ,且與圓
,且與圓![]() 外切于點
外切于點![]() ,
,![]() 是x軸上的一個動點.
是x軸上的一個動點.
![]() 求圓C的標(biāo)準(zhǔn)方程;
求圓C的標(biāo)準(zhǔn)方程;
![]() 當(dāng)圓C上存在點Q,使
當(dāng)圓C上存在點Q,使![]() ,求實數(shù)m的取值范圍;
,求實數(shù)m的取值范圍;
![]() 當(dāng)
當(dāng)![]() 時,過P作直線PA,PB與圓C分別交于異于點P的點A,B兩點,且
時,過P作直線PA,PB與圓C分別交于異于點P的點A,B兩點,且![]() 求證:直線AB恒過定點.
求證:直線AB恒過定點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)= ![]() 的圖象可能是( )
的圖象可能是( ) 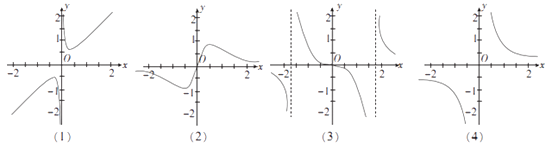
A.(1)(3)
B.(1)(2)(4)
C.(2)(3)(4)
D.(1)(2)(3)(4)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線y2=2px(p>0)上點T(3,t)到焦點F的距離為4. 
(1)求t,p的值;
(2)設(shè)A,B是拋物線上分別位于x軸兩側(cè)的兩個動點,且 ![]() (其中O為坐標(biāo)原點).求證:直線AB過定點,并求出該定點的坐標(biāo).
(其中O為坐標(biāo)原點).求證:直線AB過定點,并求出該定點的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方體ABCD-A1B1C1D1中,M,N,P分別是C1C, C1B1,C1D1的中點,點H在四邊形A1ADD1的邊及其內(nèi)部運動,則H滿足條件________時,有BH∥平面MNP.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義行列式運算 ![]() =a1b2﹣a2b1 , 將函數(shù)f(x)=
=a1b2﹣a2b1 , 將函數(shù)f(x)= ![]() 的圖象向左平移t(t>0)個單位,所得圖象對應(yīng)的函數(shù)為偶函數(shù),則t的最小值為( )
的圖象向左平移t(t>0)個單位,所得圖象對應(yīng)的函數(shù)為偶函數(shù),則t的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某園林基地培育了一種新觀賞植物,經(jīng)過一年的生長發(fā)育,技術(shù)人員從中抽取了部分植株的高度(單位:厘米)作為樣本(樣本容量為![]() )進(jìn)行統(tǒng)計,按照
)進(jìn)行統(tǒng)計,按照![]()
![]() 的分組作出頻率分布直方圖,并作出樣本高度的莖葉圖(圖中僅列出了高度在
的分組作出頻率分布直方圖,并作出樣本高度的莖葉圖(圖中僅列出了高度在![]() 的數(shù)據(jù)).
的數(shù)據(jù)).
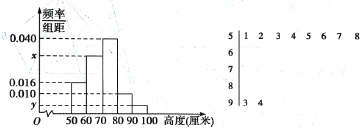
(1)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值;
的值;
(2)在選取的樣本中,從高度在![]() 厘米以上(含
厘米以上(含![]() 厘米)的植株中隨機(jī)抽取
厘米)的植株中隨機(jī)抽取![]() 株,求所取的
株,求所取的![]() 株中至少有一株高度在
株中至少有一株高度在![]() 內(nèi)的概率.
內(nèi)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=xex .
(1)求f(x)的極值;
(2)k×f(x)≥ ![]() x2+x在[﹣1,+∞)上恒成立,求k值的集合.
x2+x在[﹣1,+∞)上恒成立,求k值的集合.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下面有四個命題:
①函數(shù)y=tan x在每一個周期內(nèi)都是增函數(shù).
②函數(shù)y=sin(2x+ ![]() )的圖象關(guān)于直線x=
)的圖象關(guān)于直線x= ![]() 對稱;
對稱;
③函數(shù)y=tanx的對稱中心(kπ,0),k∈Z.
④函數(shù)y=sin(2x﹣ ![]() )是偶函數(shù).
)是偶函數(shù).
其中正確結(jié)論個數(shù)( )
A.0
B.1
C.2
D.3
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com