【題目】在△ABC中，內角A，B，C的對邊分別為a，b，c，已知
.
(1)求角C的值；
(2)若c＝2，且△ABC的面積為
，求a，b.
【答案】（1）
（2）a＝b＝2
【解析】
（1）首先利用降次公式、三角形的內角和定理、兩角和的余弦公式化簡已知條件，得到
，由此求得
的值.（2）利用三角形的面積公式和余弦定理列方程組，解方程組可求得
的值.
解：(1)2cos2
＋(cosB－
sinB)cosC＝1，故cosA＋cosBcosC－sinBcosC＝0，
則－cos(B＋C)＋cosBcosC－sinBcosC＝0，
展開得：sinBsinC－sinBcosC＝0，
∵sinB≠0，即tanC＝，∵C∈(0，π)，C＝
.
(2)三角形面積為
absin＝，故ab＝4.
由余弦定理得4＝(a＋b)2－2ab－ab，所以a＋b＝4，
故a＝b＝2.
英才計劃期末調研系列答案科目：高中數學 來源： 題型：
【題目】如圖，甲、乙兩個企業的用電負荷量
關于投產持續時間
（單位：小時）的關系
均近似地滿足函數
.
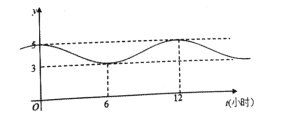
（1）根據圖象，求函數
的解析式；
（2）為使任意時刻兩企業用電負荷量之和不超過9，現采用錯峰用電的方式，讓企業乙比企業甲推遲
小時投產，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知一個幾何體是由一個直角三角形繞其斜邊旋轉一周所形成的．若該三角形的周長為12米，三邊長由小到大依次為a，b，c，且b恰好為a，c的算術平均數．
（1）求a，b，c；
（2）若在該幾何體的表面涂上一層油漆，且每平方米油漆的造價為5元，求所涂的油漆的價格．
查看答案和解析>>
科目：高中數學 來源： 題型：
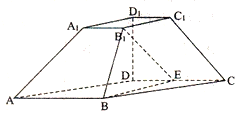
【題目】已知四棱臺
中，
平面ABCD，四邊形ABCD為平行四邊形，
，
，
，
，E為DC中點．
（1）求證：
平面
；
（2）求證：
；
（3）求三棱錐
的高．
（注：棱臺的兩底面相似）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某商場有獎銷售中，購滿100元商品得1張獎券，多購多得，100張獎券為一個開獎單位，每個開獎單位設特等獎1個，一等獎10個，二等獎50個，設一張獎券中特等獎、一等獎、二等獎的事件分別為A，B，C，可知其概率平分別為
．
（1）求1張獎券中獎的概率；
（2）求1張獎券不中特等獎且不中一等獎的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，拋物線y2=4x的焦點為F，拋物線上有三個動點A,B,C.
（1）若
，求
；
（2）若
，AB的垂直平分線經過一個定點Q，求△QAB面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
