
【題目】如圖,在平面直角坐標(biāo)系xOy中,橢圓![]() 的左、右焦點(diǎn)分別為F1,F(xiàn)2,離心率為
的左、右焦點(diǎn)分別為F1,F(xiàn)2,離心率為![]() ,兩準(zhǔn)線之間的距離為8.點(diǎn)P在橢圓E上,且位于第一象限,過點(diǎn)F1作直線PF1的垂線l1,過點(diǎn)F2作直線PF2的垂線l2.
,兩準(zhǔn)線之間的距離為8.點(diǎn)P在橢圓E上,且位于第一象限,過點(diǎn)F1作直線PF1的垂線l1,過點(diǎn)F2作直線PF2的垂線l2.
(1)求橢圓E的標(biāo)準(zhǔn)方程;
(2)若直線l1,l2的交點(diǎn)Q在橢圓E上,求點(diǎn)P的坐標(biāo).
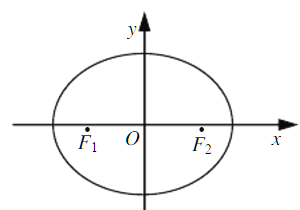
【答案】(1)∵橢圓E的離心率為![]() ,∴
,∴![]() ①.∵兩準(zhǔn)線之間的距離為8,∴
①.∵兩準(zhǔn)線之間的距離為8,∴![]() ②.聯(lián)立①②得
②.聯(lián)立①②得![]() ,∴
,∴![]() ,故橢圓E的標(biāo)準(zhǔn)方程為
,故橢圓E的標(biāo)準(zhǔn)方程為![]() .
.
(2)設(shè)![]() ,則
,則![]() ,由題意得
,由題意得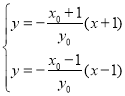 ,整理得
,整理得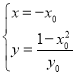 ,∵點(diǎn)
,∵點(diǎn)![]() 在橢圓E上,∴
在橢圓E上,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,故點(diǎn)P的坐標(biāo)是
,故點(diǎn)P的坐標(biāo)是![]() .
.
【解析】
解:(1)設(shè)橢圓的半焦距為c.
因?yàn)闄E圓E的離心率為![]() ,兩準(zhǔn)線之間的距離為8,所以
,兩準(zhǔn)線之間的距離為8,所以![]() ,
,![]() ,
,
解得![]() ,于是
,于是![]() ,
,
因此橢圓E的標(biāo)準(zhǔn)方程是![]() .
.
(2)由(1)知,![]() ,
,![]() .
.
設(shè)![]() ,因?yàn)辄c(diǎn)
,因?yàn)辄c(diǎn)![]() 為第一象限的點(diǎn),故
為第一象限的點(diǎn),故![]() .
.
當(dāng)![]() 時,
時,![]() 與
與![]() 相交于
相交于![]() ,與題設(shè)不符.
,與題設(shè)不符.
當(dāng)![]() 時,直線
時,直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() .
.
因?yàn)?/span>![]() ,
,![]() ,所以直線
,所以直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,
,
從而直線![]() 的方程:
的方程:![]() , ①
, ①
直線![]() 的方程:
的方程:![]() . ②
. ②
由①②,解得![]() ,所以
,所以![]() .
.
因?yàn)?/span>點(diǎn)![]() 在橢圓上,由對稱性,得
在橢圓上,由對稱性,得![]() ,即
,即![]() 或
或![]() .
.
又![]() 在橢圓E上,故
在橢圓E上,故![]() .
.
由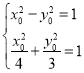 ,解得
,解得![]() ;
;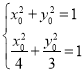 ,無解.
,無解.
因此點(diǎn)P的坐標(biāo)為![]() .
.


 云南師大附小一線名師提優(yōu)作業(yè)系列答案
云南師大附小一線名師提優(yōu)作業(yè)系列答案 沖刺100分單元優(yōu)化練考卷系列答案
沖刺100分單元優(yōu)化練考卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】張先生知道清晨從甲地到乙地有好、中、差三個班次的客車.但不知道具體誰先誰后.他打算:第一輛看后一定不坐,若第二輛比第一輛舒服,則乘第二輛;否則坐第三輛.問張先生坐到好車的概率和坐到差車的概率分別是( )
A.![]() 、
、 ![]()
B.![]() 、
、 ![]()
C.![]() 、
、 ![]()
D.![]() 、
、 ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等比數(shù)列{an}的首項(xiàng)a1= ![]() ,公比q滿足q>0且q≠1,又已知a1 , 5a3 , 9a5成等差數(shù)列;
,公比q滿足q>0且q≠1,又已知a1 , 5a3 , 9a5成等差數(shù)列;
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)令bn=log3 ![]() ,記Tn=
,記Tn= ![]() ,是否存在最大的整數(shù)m,使得對任意n∈N* , 均有Tn>
,是否存在最大的整數(shù)m,使得對任意n∈N* , 均有Tn> ![]() 成立?若存在,求出m,若不存在,請說明理由.
成立?若存在,求出m,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,內(nèi)角A、B、C所對的邊分別是a、b、c,且a+b+c=8. (Ⅰ)若a=2,b= ![]() ,求cosC的值;
,求cosC的值;
(Ⅱ)若sinAcos2 ![]() +sinBcos2
+sinBcos2 ![]() =2sinC,且△ABC的面積S=
=2sinC,且△ABC的面積S= ![]() sinC,求a和b的值.
sinC,求a和b的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC,若存在△A1B1C1 , 滿足 ![]() =
= ![]() =
= ![]() =1,則稱△A1B1C1是△ABC的一個“友好”三角形.在滿足下述條件的三角形中,存在“友好”三角形的是:(請寫出符合要求的條件的序號) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
=1,則稱△A1B1C1是△ABC的一個“友好”三角形.在滿足下述條件的三角形中,存在“友好”三角形的是:(請寫出符合要求的條件的序號) ①A=90°,B=60°,C=30°;②A=75°,B=60°,C=45°;③A=75°,B=75°,C=30°;④A=75°,B=65°,C=45°.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】袋中有質(zhì)地、大小完全相同的5個小球,編號分別為1,2,3,4,5,甲、乙兩人玩一種游戲.甲先摸出一個球.記下編號,放回后再摸出一個球,記下編號,如果兩個編號之和為偶數(shù).則算甲贏,否則算乙贏.
(1)求甲贏且編號之和為6的事件發(fā)生的概率:
(2)試問:這種游戲規(guī)則公平嗎.請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)常數(shù)![]() .
.
(1)若![]() 在
在![]() 處取得極小值為
處取得極小值為![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)對于任意給定的正實(shí)數(shù)![]() 、
、![]() ,證明:存在實(shí)數(shù)
,證明:存在實(shí)數(shù)![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個盒子裝有六張卡片,上面分別寫著如下六個函數(shù):
![]()
![]()
![]()
![]()
![]()
![]() .
.
(Ⅰ)從中任意拿取![]() 張卡片,其中至少有一張卡片上寫著的函數(shù)為奇函數(shù),在此條件下,求兩張卡片上寫著的函數(shù)相加得到的新函數(shù)為奇函數(shù)的概率;
張卡片,其中至少有一張卡片上寫著的函數(shù)為奇函數(shù),在此條件下,求兩張卡片上寫著的函數(shù)相加得到的新函數(shù)為奇函數(shù)的概率;
(Ⅱ)現(xiàn)從盒子中逐一抽取卡片,且每次取出后均不放回,若取到一張寫有偶函數(shù)的卡片則停止抽取,否則繼續(xù)進(jìn)行,求抽取次數(shù)![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com