【題目】隨著
業的迅速發展計算機也在迅速更新換代,平板電腦因使用和移動便捷以及時尚新潮性，而備受人們尤其是大學生的青睞,為了解大學生購買平板電腦進行學習的學習情況,某大學內進行了一次匿名調查,共收到1500份有效問卷.調查結果顯示700名女學生中有300人,800名男生中有400人擁有平板電腦.
(Ⅰ)完成下列列聯表：
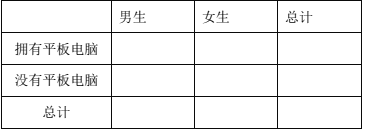
(Ⅱ)分析是否有
的把握認為購買平板電腦與性別有關?
附:獨立性檢驗臨界值表:
(參考公式:
,其中
)
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】現從某高中隨機抽取部分高二學生,調査其到校所需的時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖),其中到校所需時間的范圍是
,樣本數據分組為
.
(1)求直方圖中
的值；
(2)如果學生到校所需時間不少于1小時,則可申請在學校住宿.若該校錄取1200名新生,請估計高二新生中有多少人可以申請住宿；
(3)以直方圖中的頻率作為概率,現從該學校的高二新生中任選4名學生,用
表示所選4名學生中“到校所需時間少于40分鐘”的人數,求的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數φ（x）= 
，a＞0
（1）若函數f（x）=lnx+φ（x），在（1，2）上只有一個極值點，求a的取值范圍；
（2）若g（x）=|lnx|+φ（x），且對任意x1 ， x2∈（0，2]，且x1≠x2 ， 都有 
＜﹣1，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓 
+ 
=1（a＞b＞0）的左焦點為F，右頂點為A，離心率為 
．已知A是拋物線y2=2px（p＞0）的焦點，F到拋物線的準線l的距離為 ．
（Ⅰ）求橢圓的方程和拋物線的方程；
（Ⅱ）設l上兩點P，Q關于x軸對稱，直線AP與橢圓相交于點B（B異于A），直線BQ與x軸相交于點D．若△APD的面積為 
，求直線AP的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】微信是現代生活進行信息交流的重要工具，據統計，某公司
名員工中
的人使用微信，其中每天使用微信時間在一小時以內的有
，其余的員工每天使用微信的時間在一小時以上，若將員工分成青年（年齡小于
歲）和中年（年齡不小于歲）兩個階段，那么使用微信的人中
是青年人.若規定：每天使用微信時間在一小時以上為經常使用微信，那么經常使用微信的員工中
是青年人.
（1）若要調查該公司使用微信的員工經常使用微信與年齡的關系，列出
列聯表：
青年人 | 中年人 | 總計 | |
經常使用微信 | |||
不經常使用微信 | |||
總計 |
（2）由列聯表中所得數據判斷，是否有百分之
的把握認為“經常使用微信與年齡有關”？
| 0.010 | 0.001 |
| 6.635 | 10.828 |
附：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
經過點
，且圓心在直線
：
上.
（1）求圓的方程；
（2）過點
的直線與圓交于
兩點，問在直線
上是否存在定點
，使得
恒成立？若存在，請求出點的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
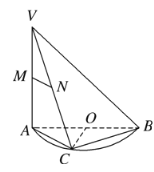
【題目】如圖所示，
是半圓
的直徑，
垂直于半圓所在的平面，點
是圓周上不同于
的任意一點，
分別為
的中點，則下列結論正確的是( )
A.
B.平面
平面
C.
與
所成的角為45°D.
平面
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在ABC中，角A，B，C的對邊分別為a，b，c，若△ABC為銳角三角形，且滿足sinB（1+2cosC）=2sinAcosC+cosAsinC，則下列等式成立的是（ ）
A.a=2b
B.b=2a
C.A=2B
D.B=2A
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】△ABC的內角A，B，C的對邊分別為a，b，c，已知sin（A+C）=8sin2 
．
（Ⅰ）求cosB；
（Ⅱ）若a+c=6，△ABC面積為2，求b．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
