
已知函數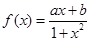 是定義域為
是定義域為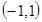 上的奇函數,且
上的奇函數,且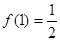
(1)求 的解析式,
的解析式,
(2)用定義證明: 在
在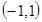 上是增函數,
上是增函數,
(3)若實數 滿足
滿足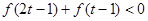 ,求實數
,求實數 的范圍.
的范圍.
(1)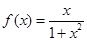 ;(2)見解析;(3) 0<
;(2)見解析;(3) 0<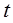 <
<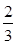
 。
。
解析試題分析:(1)先根據f(x)為奇函數,知f(0)=0,可得b=0,然后再根據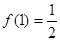 ,求出a值.從而確定f(x)的解析式.
,求出a值.從而確定f(x)的解析式.
(2)用單調性定義證明函數單調性的步驟有三:一是取值.二是作差變形,判斷符號;三是得出結論.
(3)解此類抽象不等式關鍵是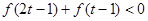 ∴
∴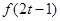 <-
<-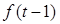 ,再根據奇函數轉化為
,再根據奇函數轉化為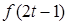 <
<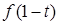 ,再利用單調性脫掉法則符號f,從而轉化為自變量之間的大小關系即可解決.
,再利用單調性脫掉法則符號f,從而轉化為自變量之間的大小關系即可解決.
(1) ∵函數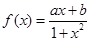 是定義域為
是定義域為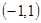 上的奇函數 ∴
上的奇函數 ∴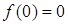
∴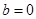 ——————————2
——————————2
又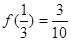 ∴
∴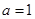
∴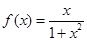 ——————————————4
——————————————4
(2)任取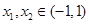 且
且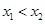
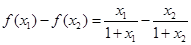
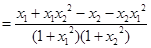
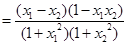 ————————6
————————6
∵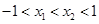 ∴
∴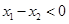
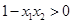
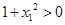
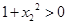
∴ 即
即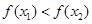
∴  在
在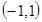 上是增函數————————————8
上是增函數————————————8
(3)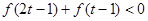 ∴
∴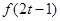 <-
<-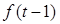
又由已知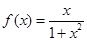 是
是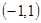 上的奇函數
上的奇函數
∴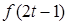 <
<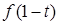 ----------------------10
----------------------10
∵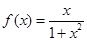 是
是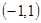 上的增函數
上的增函數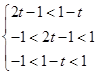 ————————————13
————————————13
∴0<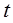 <
<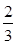
 --------------------------------14
--------------------------------14
考點:本小題考查函數的奇偶性和單調性以及解抽象不等式等知識.
點評: 當奇函數的定義域內有0時,要注意f(0)=0這個條件的使用.利用單調性定義進行證明時,關鍵是作差變形確定差值符號,一般要分解成若干個因式積的形式,通過判斷每個因式的符號來判斷差值符號.
在解抽象不等式時,要注意利用單調性把函數值的大小關系轉化為自變量之間的大小關系從而轉化為普通不等式來解.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:解答題
(附加題)本小題滿分10分
已知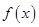 是定義在
是定義在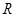 上單調函數,對任意實數
上單調函數,對任意實數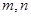 有:
有: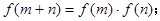 且
且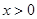 時,
時,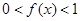 .
.
(1)證明: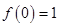 ;
;
(2)證明:當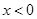 時,
時,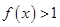 ;
;
(3)當 時,求使
時,求使 對任意實數
對任意實數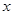 恒成立的參數
恒成立的參數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(16分)已知函數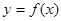 是定義在
是定義在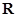 上的奇函數,且當
上的奇函數,且當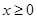 時,
時, .
.
(1)當 時,求函數
時,求函數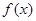 的解析式;
的解析式;
(2)若函數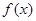 為單調遞減函數;
為單調遞減函數;
①直接寫出 的范圍(不必證明);
的范圍(不必證明);
②若對任意實數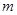 ,
,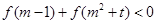 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)是定義在(0,+∞)上的單調增函數,滿足f(xy)=f(x)+f(y),f(3)=1
(1)求f(1)的值
(2)若滿足f(x) +f(x-8)≤2 求x的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com