
【題目】已知函數![]() ,
,![]() .
.
(1)若不等式![]() 對任意的
對任意的![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)記![]() 表示
表示![]() 中的最小值,若函數
中的最小值,若函數![]() 在
在![]() 內恰有一個零點,求實
內恰有一個零點,求實![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)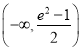
【解析】
(1)利用分離參數,并構造新的函數![]() ,利用導數判斷
,利用導數判斷![]() 的單調性,并求最值,可得結果.
的單調性,并求最值,可得結果.
(2)利用對![]() 的分類討論,可得
的分類討論,可得![]() ,然后判斷函數單調性以及根據零點存在性定理,可得結果.
,然后判斷函數單調性以及根據零點存在性定理,可得結果.
(1)由![]() ,得
,得![]() ,
,
令![]() ,
,
![]()
當![]() 時,
時,
![]() ,
,![]() ,
,![]() ;
;
當![]() 時,
時,
![]() ,
,![]() ,
,![]() ,
,
∴函數![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,
上遞增,
![]() ,
,![]() ,
,
∴實數![]() 的取值范圍是
的取值范圍是![]()
(2) ①由(1) 得當![]() 時,
時,![]() ,
,
![]() ,
,
![]() ,
,
函數![]() 在
在![]() 內恰有一個零點
內恰有一個零點![]() ,符合題意
,符合題意
②當![]() 時,
時,
i.若![]() ,
,![]() ,
,
![]() ,
,
故函數![]() 在
在![]() 內無零點
內無零點
ii.若![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 不是函數
不是函數![]() 的零點;
的零點;
iii.若![]() 時,
時,![]() ,
,
故只考慮函數![]() 在
在![]() 的零點,
的零點,![]() ,
,
若![]() 時,
時,
![]() ,∴函數
,∴函數![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,
,
![]() ,
,
∴函數![]() 在
在![]() 上恰有一個零點
上恰有一個零點
若![]() 時,
時,
![]() , ∴函數
, ∴函數![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() ,∴函數
,∴函數![]() 在
在![]() 上無零點,
上無零點,
若![]() 時,
時,
![]() ,
,![]() ,
,
∴函數![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,
上遞增,
要使![]() 在
在![]() 上恰有一個零點, 只需
上恰有一個零點, 只需![]() ,
,
![]() .
.
綜上所述,實數![]() 的取值范圍是
的取值范圍是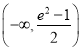 .
.


 寒假學與練系列答案
寒假學與練系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
以直角坐標系的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知點
軸的正半軸為極軸建立極坐標系,已知點![]() 的直角坐標為
的直角坐標為![]() ,若直線
,若直線![]() 的極坐標方程為
的極坐標方程為![]() 曲線
曲線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).
為參數).
(1)求直線![]() 和曲線
和曲線![]() 的普通方程;
的普通方程;
(2)設直線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,求
兩點,求![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為平面直角坐標系的原點,極軸為
,以極點為平面直角坐標系的原點,極軸為![]() 軸的正半軸,建立平面直角坐標系,曲線C的參數方程是
軸的正半軸,建立平面直角坐標系,曲線C的參數方程是![]() ,(
,(![]() 為參數).
為參數).
(1)求直線![]() 被曲線C截得的弦長;
被曲線C截得的弦長;
(2)從極點作曲線C的弦,求各弦中點軌跡的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《基礎教育課程改革綱要(試行)》將“具有良好的心理素質”列入新課程的培養目標.為加強心理健康教育工作的開展,不斷提高學生的心理素質,九江市某校高二年級開設了《心理健康》選修課,學分為2分.學校根據學生平時上課表現給出“合格”與“不合格”兩種評價,獲得“合格”評價的學生給予50分的平時分,獲得“不合格”評價的學生給予30分的平時分,另外還將進行一次測驗.學生將以“平時分×40%+測驗分×80%”作為“最終得分”,“最終得分”不少于60分者獲得學分.
該校高二(1)班選修《心理健康》課的學生的平時份及測驗分結果如下:
測驗分 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
平時分50分人數 | 0 | 3 | 4 | 4 | 2 | ||
平時分30分人數 | 1 | 0 | 0 |
(1)根據表中數據完成如下2×2列聯表,并分析是否有95%的把握認為這些學生“測驗分是否達到60分”與“平時分”有關聯?
選修人數 | 測驗分 達到60分 | 測驗分 未達到60分 | 合計 |
平時分50分 | |||
平時分30分 | |||
合計 |
(2)若從這些學生中隨機抽取1人,求該生獲得學分的概率.
附: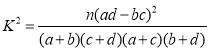 ,其中
,其中![]()
| 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市調查機構在某設置過街天橋的路口隨機調查了110人準備過馬路的交通參與者對跨越護欄和走過街天橋的看法,得到如下列聯表:
男 | 女 | 合計 | |
走過街天橋 | 40 | 20 | 60 |
跨越護欄 | 20 | 30 | 50 |
合計 | 60 | 50 | 110 |
附:![]() .
.
| 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
則可以得到正確的結論是( )
A.有99%以上的把握認為“選擇過馬路的方式與性別有關”
B.有99%以上的把握認為“選擇過馬路的方式與性別無關”
C.在犯錯誤的概率不超過0.1%的前提下,認為“選擇過馬路的方式與性別有關”
D.在犯錯誤的概率不超過0.1%的前提下,認為“選擇過馬路的方式與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐P﹣ABC中,AC⊥BC,AC=BC=2,PA=PB=PC=3,O是AB中點,E是PB中點.
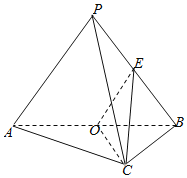
(1)證明:平面PAB⊥平面ABC;
(2)求點B到平面OEC的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com