
【題目】
如圖,已知平面QBC與直線PA均垂直于![]() 所在平面,且PA=AB=AC.
所在平面,且PA=AB=AC.
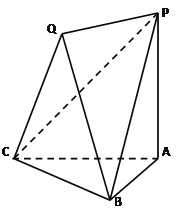
(Ⅰ)求證:PA∥平面QBC;
(Ⅱ)若![]() ,求二面角Q-PB-A的余弦值.
,求二面角Q-PB-A的余弦值.
【答案】(1)通過已知中的平面![]() ⊥平面
⊥平面![]() ,那么結(jié)合
,那么結(jié)合![]() 平面
平面![]() ,和
,和![]() ⊥平面
⊥平面![]() ,從而得到線線平行
,從而得到線線平行![]() ∥
∥![]() ,利用線面平行的性質(zhì)來證明.
,利用線面平行的性質(zhì)來證明.
(2)![]()
【解析】
試題解:(I)證明:過點![]() 作
作![]() 于點
于點![]() ,
,
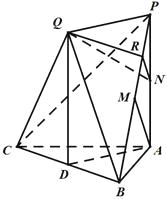
∵平面![]() ⊥平面
⊥平面![]() ∴
∴![]() 平面
平面![]()
又∵![]() ⊥平面
⊥平面![]()
∴![]() ∥
∥![]() 又∵
又∵![]() 平面
平面![]()
∴![]() ∥平面
∥平面![]()
(Ⅱ)∵![]() 平面
平面![]()
∴![]() 又∵
又∵![]()
∴![]() ∴
∴![]()
∴點![]() 是
是![]() 的中點,連結(jié)
的中點,連結(jié)![]() ,則
,則![]()
∴![]() 平面
平面![]() ∴
∴![]() ∥
∥![]() ,
,![]()
∴四邊形![]() 是矩形
是矩形
設(shè)![]()
∴![]() ,
,![]() ∴
∴![]()
過![]() 作
作![]() 于點
于點![]() ,
,
∴![]() ,
,![]()
取![]() 中點
中點![]() ,連結(jié)
,連結(jié)![]() ,取
,取![]() 的中點
的中點![]() ,連結(jié)
,連結(jié)![]()
∵![]() ,
,![]() ∴
∴![]() ∥
∥![]()
∵![]() ∴
∴![]() ∴
∴![]()
∴![]() 為二面角
為二面角![]() 的平面角
的平面角
連結(jié)![]() ,則
,則![]() 又∵
又∵![]()
∴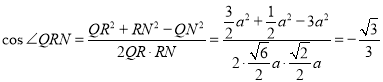
即二面角![]() 的余弦值為
的余弦值為![]()
方法二:
(I)同方法一
(Ⅱ)∵![]() 平面
平面![]()
∴![]() ,又∵
,又∵![]()
∴![]() ∴
∴![]()
∴點![]() 是
是![]() 的中點,連結(jié)
的中點,連結(jié)![]() ,則
,則![]()
∴![]() 平面
平面![]() ∴
∴![]() ∥
∥![]() ,
,![]()
∴四邊形![]() 是矩形
是矩形
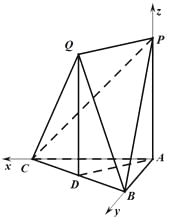
分別以![]() 為
為![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]()
設(shè)![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]()
∵![]() ,
,![]()
∴![]()
又∵平面![]() 的法向量為
的法向量為![]()
設(shè)二面角![]() 為
為![]() ,則
,則
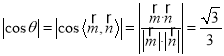
又∵二面角![]() 是鈍角
是鈍角
∴![]()


科目:高中數(shù)學 來源: 題型:
【題目】在極坐標系中,已知曲線![]() :
:![]() 和曲線
和曲線![]() :
:![]() ,以極點
,以極點![]() 為坐標原點,極軸為
為坐標原點,極軸為![]() 軸非負半軸建立平面直角坐標系.
軸非負半軸建立平面直角坐標系.
(1)求曲線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 是曲線
是曲線![]() 上一動點,過點
上一動點,過點![]() 作線段
作線段![]() 的垂線交曲線
的垂線交曲線![]() 于點
于點![]() ,求線段
,求線段![]() 長度的最小值.
長度的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】基于移動網(wǎng)絡(luò)技術(shù)的共享單車被稱為“新四大發(fā)明”之一,短時間內(nèi)就風靡全國,給人們帶來新的出行體驗,某共享單車運營公司的市場研究人員為了了解公司的經(jīng)營狀況,對公司最近6個月的市場占有率![]() 進行了統(tǒng)計,結(jié)果如下表:
進行了統(tǒng)計,結(jié)果如下表:
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
(1)請用相關(guān)系數(shù)說明能否用線性回歸模型擬合![]() 與月份代碼
與月份代碼![]() 之間的關(guān)系.如果能,請計算出
之間的關(guān)系.如果能,請計算出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程,如果不能,請說明理由;
的線性回歸方程,如果不能,請說明理由;
(2)根據(jù)調(diào)研數(shù)據(jù),公司決定再采購一批單車擴大市場,從成本1000元/輛的![]() 型車和800元/輛的
型車和800元/輛的![]() 型車中選購一種,兩款單車使用壽命頻數(shù)如下表:
型車中選購一種,兩款單車使用壽命頻數(shù)如下表:
| 1年 | 2年 | 3年 | 4年 | 總計 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
經(jīng)測算,平均每輛單車每年能為公司帶來500元的收入,不考慮除采購成本以外的其它成本,假設(shè)每輛單車的使用壽命都是整數(shù)年,用頻率估計每輛車使用壽命的概率,以平均每輛單車所產(chǎn)生的利潤的估計值為決策依據(jù),如果你是公司負責人,會選擇哪款車型?
參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:相關(guān)系數(shù)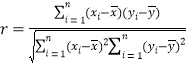 ,
, ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】![]() 年
年![]() 月
月![]() 日,小劉從各個渠道融資
日,小劉從各個渠道融資![]() 萬元,在某大學投資一個咖啡店,
萬元,在某大學投資一個咖啡店,![]() 年
年![]() 月
月![]() 日正式開業(yè),已知開業(yè)第一年運營成本為
日正式開業(yè),已知開業(yè)第一年運營成本為![]() 萬元,由于工人工資不斷增加及設(shè)備維修等,以后每年成本增加
萬元,由于工人工資不斷增加及設(shè)備維修等,以后每年成本增加![]() 萬元,若每年的銷售額為
萬元,若每年的銷售額為![]() 萬元,用數(shù)列
萬元,用數(shù)列![]() 表示前
表示前![]() 年的純收入.(注:純收入
年的純收入.(注:純收入![]() 前
前![]() 年的總收入
年的總收入![]() 前
前![]() 年的總支出
年的總支出![]() 投資額)
投資額)
(1)試求年平均利潤最大時的年份(年份取正整數(shù))并求出最大值.
(2)若前![]() 年的收入達到最大值時,小劉計劃用前
年的收入達到最大值時,小劉計劃用前![]() 年總收入的
年總收入的![]() 對咖啡店進行重新裝修,請問:小劉最早從哪一年對咖啡店進行重新裝修(年份取整數(shù))?并求小劉計劃裝修的費用.
對咖啡店進行重新裝修,請問:小劉最早從哪一年對咖啡店進行重新裝修(年份取整數(shù))?并求小劉計劃裝修的費用.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() ,過拋物線C的焦點F作互相垂直的兩條直線AB,CD,與拋物線C分別相交于A,B和C,D,點A,C在x軸上方.
,過拋物線C的焦點F作互相垂直的兩條直線AB,CD,與拋物線C分別相交于A,B和C,D,點A,C在x軸上方.
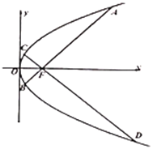
(1)若直線AB的傾斜角為![]() ,求
,求![]() 的值;
的值;
(2)設(shè)![]() 與
與![]() 的面積之和為S,求S的最小值.
的面積之和為S,求S的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若不等式![]() 對任意的
對任意的![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)記![]() 表示
表示![]() 中的最小值,若函數(shù)
中的最小值,若函數(shù)![]() 在
在![]() 內(nèi)恰有一個零點,求實
內(nèi)恰有一個零點,求實![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(Ⅰ)記![]() ,試判斷函數(shù)
,試判斷函數(shù)![]() 的極值點的情況;
的極值點的情況;
(Ⅱ)若![]() 有且僅有兩個整數(shù)解,求實數(shù)
有且僅有兩個整數(shù)解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】每年暑期都會有大量中學生參加名校游學,夏令營等活動,某中學學生社團將其今年的社會實踐主題定為“中學生暑期游學支出分析”,并在該市各個中學隨機抽取了共![]() 名中學生進行問卷調(diào)查,根據(jù)問卷調(diào)查發(fā)現(xiàn)共
名中學生進行問卷調(diào)查,根據(jù)問卷調(diào)查發(fā)現(xiàn)共![]() 名中學生參與了各類游學、夏令營等活動,從中統(tǒng)計得到中學生暑期游學支出(單位:百元)頻率分布方圖如圖.
名中學生參與了各類游學、夏令營等活動,從中統(tǒng)計得到中學生暑期游學支出(單位:百元)頻率分布方圖如圖.
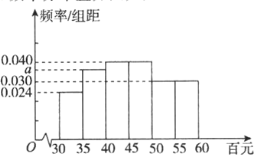
(I)求實數(shù)![]() 的值;
的值;
(Ⅱ)在![]() ,
,![]() ,
,![]() 三組中利用分層抽樣抽取
三組中利用分層抽樣抽取![]() 人,并從抽取的
人,并從抽取的![]() 人中隨機選出
人中隨機選出![]() 人,對其消費情況進行進一步分析.
人,對其消費情況進行進一步分析.
(i)求每組恰好各被選出![]() 人的概率;
人的概率;
(ii)設(shè)![]() 為選出的
為選出的![]() 人中
人中![]() 這一組的人數(shù),求隨機變量
這一組的人數(shù),求隨機變量![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com