正方形
ABCD邊長為2,
E、
F分別是
AB和
CD的中點,將正方形沿
EF折成直二面角(如圖),
M為矩形
AEFD內(nèi)一點,如果∠
MBE=∠
MBC,
MB和平面
BCF所成角的正切值為
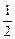
,那么點
M到直線
EF的距離為( )
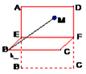
過點
M作
MM′⊥
EF,則
MM′⊥平面
BCF∵∠
MBE=∠
MBC ∴
BM′為∠
EBC為角平分線,
∴∠
EBM′=45°,
BM′=

,從而
MN=

,故選A。
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
在棱長為
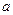
的正方體

中,
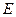
為棱
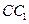
的中點.
(Ⅰ)求證:
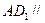
平面
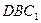
; (Ⅱ)求
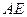
與平面
所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,ABCD是正方形,O是正方形的中心,PO
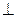
底面ABCD,E是PC的中點。
求證:(1)PA∥平面BDE
(2)平面PAC
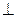
平面BDE
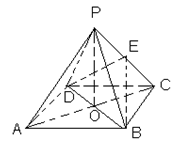
(3)求二面角E-BD-A的大小。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
等邊ABC的A∈平面α,B、C到面α的距離分別為2a、a,且AB=BC=AC=b.
(1)求面ABC與α所成二面角的大小;
(2)若B、C到α的距離分別為3a、a呢?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
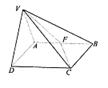
如圖,平面VAD⊥平面ABCD,△VAD是等邊三角形,ABCD是矩形,AB∶AD=
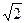
∶1,F(xiàn)是AB的中點.
(1)求VC與平面ABCD所成的角;
(2)求二面角V-FC-B的度數(shù);
(3)當V到平面ABCD的距離是3時,求B到平面VFC的距離.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,底面是正方形的四棱錐
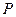
–
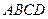
,平面
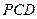
⊥平面
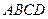
,
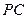
=
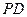
=
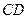
=2.
(I)求證:
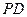
⊥
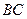
;
(II)求直線
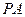
與平面
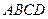
所成的角的正弦值.
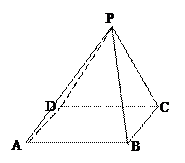
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(1)當你手握直角三角板,其斜邊保持不動,將其直角頂點提起一點,則直角在平面內(nèi)的正投影是銳角、直角 還是鈍角?
(2)根據(jù)第(1)題,你能猜想某個角在一個平面內(nèi)的正投影一定大于這個角嗎?如果正確,請證明;如果錯誤,則利用下列三角形舉出反例:△ABC中,
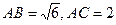
,
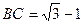
,以∠BAC為例。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖所示,已知四棱錐
S—ABCD的底面
ABCD是矩形,
M、
N分別是
CD、
SC的中點,
SA⊥底面
ABCD,
SA=
AD=1,
AB=
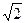
.
(1)求證:
MN⊥平面
ABN;
(2)求二面角
A—BN—
C的余弦值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
軸截面是直角三角形的圓錐的底面半徑為r,則其軸截面面積為________.
查看答案和解析>>

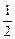 ,那么點M到直線EF的距離為( )
,那么點M到直線EF的距離為( )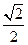
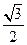
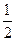

 底面ABCD,E是PC的中點。
底面ABCD,E是PC的中點。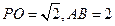
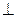 平面BDE
平面BDE (3)求二面角E-BD-A的大小。
(3)求二面角E-BD-A的大小。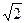 ∶1,F(xiàn)是AB的中點.
∶1,F(xiàn)是AB的中點.
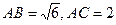 ,
,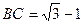 ,以∠BAC為例。
,以∠BAC為例。 .
.