
【題目】如圖,在棱長為3的正方體ABCD﹣A1B1C1D1中,A1E=CF=1. 
(1)求兩條異面直線AC1與D1E所成角的余弦值;
(2)求直線AC1與平面BED1F所成角的正弦值.
【答案】
(1)解:以D為原點,建立空間直角坐標(biāo)系D﹣xyz如圖所示:
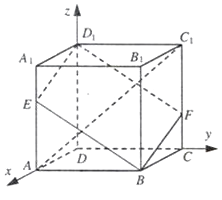
則A(3,0,0),C1=(0,3,3),D1=(0,0,3),E(3,0,2)
∴ ![]() =(﹣3,3,3),
=(﹣3,3,3), ![]() =(3,0,﹣1)
=(3,0,﹣1)
∴cosθ=  =
= ![]() =﹣
=﹣ ![]()
則兩條異面直線AC1與D1E所成角的余弦值為 ![]()
(2)解:B(3,3,0), ![]() =(0,﹣3,2),
=(0,﹣3,2), ![]() =(3,0,﹣1)
=(3,0,﹣1)
設(shè)平面BED1F的一個法向量為 ![]() =(x,y,z)
=(x,y,z)
由  得
得 ![]()
令x=1,則 ![]() =(1,2,3)
=(1,2,3)
則直線AC1與平面BED1F所成角的正弦值為
| 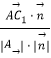 |=
|= ![]() =
= ![]()
【解析】(1)以以D為原點,建立空間直角坐標(biāo)系D﹣xyz,則我們易求出已知中,各點的坐標(biāo),進(jìn)而求出向量 ![]() ,
, ![]() 的坐標(biāo).代入向量夾角公式,結(jié)合異面直線夾角公式,即可得到答案.(2)設(shè)出平面BED1F的一個法向量為
的坐標(biāo).代入向量夾角公式,結(jié)合異面直線夾角公式,即可得到答案.(2)設(shè)出平面BED1F的一個法向量為 ![]() ,根據(jù)法向量與平面內(nèi)任一向量垂直,數(shù)量積為0,構(gòu)造方程組,求出平面BED1F的法向量為
,根據(jù)法向量與平面內(nèi)任一向量垂直,數(shù)量積為0,構(gòu)造方程組,求出平面BED1F的法向量為 ![]() 的坐標(biāo),代入線面夾角向量公式,即可求出答案.
的坐標(biāo),代入線面夾角向量公式,即可求出答案.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)的定義域是(0, ![]() ),f′(x)是它的導(dǎo)函數(shù),且f(x)+tanxf′(x)>0在定義域內(nèi)恒成立,則( )
),f′(x)是它的導(dǎo)函數(shù),且f(x)+tanxf′(x)>0在定義域內(nèi)恒成立,則( )
A.f( ![]() )>
)> ![]() f(
f( ![]() )
)
B.![]() sin1?f(1)>f(
sin1?f(1)>f( ![]() )
)
C.f( ![]() )>
)> ![]() f(
f( ![]() )
)
D.![]() f(
f( ![]() )>
)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知實數(shù)a,b,c滿足a,b,c∈R+ .
(Ⅰ)若ab=1,證明:( ![]() +
+ ![]() )2≥4;
)2≥4;
(Ⅱ)若a+b+c=3,且 ![]() +
+ ![]() +
+ ![]() ≤|2x﹣1|﹣|x﹣2|+3恒成立,求x的取值范圍.
≤|2x﹣1|﹣|x﹣2|+3恒成立,求x的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列結(jié)論正確的是( )
A.命題“若![]() ,則
,則![]() ”為假命題
”為假命題
B.命題“若![]() ,則
,則![]() ”的否命題為假命題
”的否命題為假命題
C.命題“若![]() ,則方程
,則方程![]() 有實根”的逆命題為真命題
有實根”的逆命題為真命題
D.命題“若![]() ,則
,則![]() ”的逆否命題為真命題
”的逆否命題為真命題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(已知函數(shù)f(x)=|2x+1|+|x﹣2|,不等式f(x)≤2的解集為M.
(1)求M;
(2)記集合M的最大元素為m,若正數(shù)a,b,c滿足abc=m, 求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為 ![]() ,左、右焦點分別為圓F1、F2 , M是C上一點,|MF1|=2,且|
,左、右焦點分別為圓F1、F2 , M是C上一點,|MF1|=2,且| ![]() ||
|| ![]() |=2
|=2 ![]() .
.
(1)求橢圓C的方程;
(2)當(dāng)過點P(4,1)的動直線l與橢圓C相交于不同兩點A、B時,線段AB上取點Q,且Q滿足| ![]() ||
|| ![]() |=|
|=| ![]() ||
|| ![]() |,證明點Q總在某定直線上,并求出該定直線的方程.
|,證明點Q總在某定直線上,并求出該定直線的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國“一帶一路”戰(zhàn)略構(gòu)思提出后, 某科技企業(yè)為抓住“一帶一路”帶來的機遇, 決定開發(fā)生產(chǎn)一款大型電子設(shè)備, 生產(chǎn)這種設(shè)備的年固定成本為![]() 萬元, 每生產(chǎn)
萬元, 每生產(chǎn)![]() 臺,需另投入成本
臺,需另投入成本![]() (萬元), 當(dāng)年產(chǎn)量不足
(萬元), 當(dāng)年產(chǎn)量不足![]() 臺時,
臺時,![]() (萬元); 當(dāng)年產(chǎn)量不小于
(萬元); 當(dāng)年產(chǎn)量不小于![]() 臺時
臺時![]() (萬元), 若每臺設(shè)備售價為
(萬元), 若每臺設(shè)備售價為![]() 萬元, 通過市場分析,該企業(yè)生產(chǎn)的電子設(shè)備能全部售完.
萬元, 通過市場分析,該企業(yè)生產(chǎn)的電子設(shè)備能全部售完.
(1)求年利潤![]() (萬元)關(guān)于年產(chǎn)量
(萬元)關(guān)于年產(chǎn)量![]() (臺)的函數(shù)關(guān)系式;
(臺)的函數(shù)關(guān)系式;
(2)年產(chǎn)量為多少臺時 ,該企業(yè)在這一電子設(shè)備的生產(chǎn)中所獲利潤最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以直角坐標(biāo)系的原點O為極點,x軸的正半軸為極軸,且兩個坐標(biāo)系取相等的長度單位,已知直線l的參數(shù)方程為 ![]() (t為參數(shù),0<φ<π),曲線C的極坐標(biāo)方程為ρcos2θ=8sinθ.
(t為參數(shù),0<φ<π),曲線C的極坐標(biāo)方程為ρcos2θ=8sinθ.
(1)求直線l的普通方程和曲線C的直角坐標(biāo)方程;
(2)設(shè)直線l與曲線C相交于A、B兩點,當(dāng)φ變化時,求|AB|的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 如圖,長方體ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,點E,F分別在A1B1,D1C1上,A1E=D1F=4.過點E,F的平面
如圖,長方體ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,點E,F分別在A1B1,D1C1上,A1E=D1F=4.過點E,F的平面![]() 與此長方體的面相交,交線圍成一個正方形。
與此長方體的面相交,交線圍成一個正方形。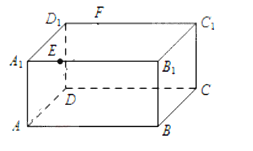
(1)(I)在圖中畫出這個正方形(不必說明畫法與理由);
(2)(II)求平面 把該長方體分成的兩部分體積的比值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com