
【題目】正三棱柱![]() 的底邊長為2,
的底邊長為2, ![]() 分別為
分別為![]() 的中點.
的中點.
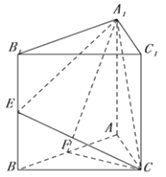
(1)已知![]() 為線段
為線段![]() 上的點,且
上的點,且![]() ,求證:
,求證: ![]() 面
面![]() ;
;
(2)若二面角![]() 的余弦值為
的余弦值為![]() ,求
,求![]() 的值.
的值.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(I)取B1A1中點為N,連結BN,推導出BN∥A1F,從而EM∥BN,進而EM∥A1F,由此能證明EM∥面A1FC.
(II)以F為坐標原點建立空間直角坐標系,設AA1=a,利用向量法能求出結果.
試題解析:
證明:(1)取![]() 中點為N,連結BN
中點為N,連結BN

則BN∥![]() F,又
F,又![]() =4
=4![]() M,
M,
則EM∥BN,所以EM∥![]() F,
F,
因為EM面![]() FC,
FC, ![]() F面
F面![]() FC,
FC,
故EM∥面![]() FC.
FC.
(2)如圖,以F為坐標原點建立空間直角坐標系,設A![]() =a.
=a.
則F(0,0,0), ![]() (1,0,a),E(1,0,a2),C(0,
(1,0,a),E(1,0,a2),C(0, ![]() ,0),
,0),
![]() (1,
(1, ![]() ,
,![]() ),
),![]() (0,
(0, ![]() ,0),
,0), ![]() (2,0,
(2,0, ![]() ),
),![]() (1,
(1, ![]() ,a),
,a),
設平面![]() CF法向量為
CF法向量為![]() ,
,
設平面![]() EF法向量為
EF法向量為![]()
則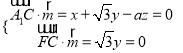 ,取z=1,得
,取z=1,得![]() =(a,0,1),
=(a,0,1),
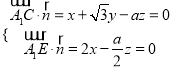 ,取x=1,得
,取x=1,得![]() =(a,
=(a, ![]() a,4);
a,4);
設二面角E![]() CF的平面角為θ,
CF的平面角為θ,
∵二面角E![]() CF所成角的余弦值為
CF所成角的余弦值為![]() ,
,
所以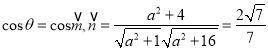
解得![]()
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】我國古代數學著作《九章算術》有如下問題:“今有蒲(水生植物名)生一日,長三尺;莞(植物名,俗稱水蔥、席子草)生一日,長一尺.蒲生日自半,莞生日自倍.問幾何日而長等?”意思是:今有蒲生長1日,長為3尺;莞生長1日,長為1尺.蒲的生長逐日減半,莞的生長逐日增加1倍.若蒲、莞長度相等,則所需的時間約為( )(結果保留一位小數.參考數據:![]() ,
,![]() )( )
)( )
A. 1.3日 B. 1.5日 C. 2.6日 D. 2.8日
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 在圓
在圓![]() 上,
上, ![]() 的坐標分別為
的坐標分別為![]() ,
, ![]() ,線段
,線段![]() 的垂直平分線交線段
的垂直平分線交線段![]() 于點
于點![]()
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設圓![]() 與點
與點![]() 的軌跡
的軌跡![]() 交于不同的四個點
交于不同的四個點![]() ,求四邊形
,求四邊形![]() 的面積的最大值及相應的四個點的坐標.
的面積的最大值及相應的四個點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品的三個質量指標分別為x,y,z,用綜合指標S=x+y+z評價該產品的等級.若S≤4,則該產品為一等品.現從一批該產品中,隨機抽取10件產品作為樣本,其質量指標列表如下:
產品編號 | A1 | A2 | A3 | A4 | A5 |
質量指標 | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
產品編號 | A6 | A7 | A8 | A9 | A10 |
質量指標 | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(1)利用上表提供的樣本數據估計該批產品的一等品率.
(2)在該樣品的一等品中,隨機抽取2件產品, ①用產品編號列出所有可能的結果;
②設事件B為“在取出的2件產品中,每件產品的綜合指標S都等于4”,求事件B發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4-4 坐標系與參數方程) 以平面直角坐標系的原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,設曲線C的參數方程為
軸的正半軸為極軸建立極坐標系,設曲線C的參數方程為 (
(![]() 是參數),直線
是參數),直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的直角坐標方程和曲線C的普通方程;
的直角坐標方程和曲線C的普通方程;
(2)設點P為曲線C上任意一點,求點P到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數y=f(x)的定義域是[0,4],則函數g(x)= ![]() 的定義域是( )
的定義域是( )
A.[0,2]
B.[0,2)
C.[0,1)∪(1,2]
D.[0,4]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某賓館有相同標準的床位100張,根據經驗,當該賓館的床價(即每張床位每天的租金)不超過10元時,床位可以全部租出;當床位高于10元時,每提高1元,將有3張床位空閑. 為了獲得較好的效益,該賓館要給床位定一個合適的價格,條件是:①要方便結帳,床價應為1元的整數倍;②該賓館每日的費用支出為575元,床位出租的收入必須高于支出,而且高得越多越好.若用x表示床價,用y表示該賓館一天出租床位的凈收入(即除去每日的費用支出后的收入):
(1)把y表示成x的函數;
(2)試確定,該賓館將床價定為多少元時,既符合上面的兩個條件,又能使凈收入高?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為考察高中生的性別與喜歡數學課程之間的關系,在某學校高中生中隨機抽取了250名學生,得到如圖的二維條形圖.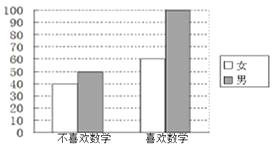
(1)根據二維條形圖,完成下表:
男 | 女 | 合計 | |
喜歡數學課程 | |||
不喜歡數學課程 | |||
合計 |
(2)對照如表,利用列聯表的獨立性檢驗估計,請問有多大把握認為“性別與喜歡數學有關系”?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求實數a的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com