
【題目】已知函數![]() ,
, ![]()
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)若函數![]() 在區間
在區間![]() 上有1個零點,求實數
上有1個零點,求實數![]() 的取值范圍;
的取值范圍;
(3)是否存在正整數![]() ,使得
,使得![]() 在
在![]() 上恒成立?若存在,求出k的最大值;若不存在,說明理由.
上恒成立?若存在,求出k的最大值;若不存在,說明理由.
【答案】(1)見解析;(2) ![]() ;(3)見解析.
;(3)見解析.
【解析】試題分析:(1)當![]() 時,得到
時,得到![]() ,求得
,求得![]() ,利用
,利用![]() 和
和![]() ,即可求解函數的單調區間;
,即可求解函數的單調區間;
(2)由![]() ,分
,分![]() 和
和![]() 兩種情況分類討論,得到函數的單調性與極值,結合函數的圖象,即可求解實數
兩種情況分類討論,得到函數的單調性與極值,結合函數的圖象,即可求解實數![]() 的取值范圍;
的取值范圍;
(3)假設存在正整數![]() ,使得
,使得![]() 在
在![]() 上恒成立,分類參數得出
上恒成立,分類參數得出![]() 對
對![]() 恒成立,設函數
恒成立,設函數![]() ,求得
,求得![]() ,求得函數
,求得函數![]() 單調性與極值,即可求解實數
單調性與極值,即可求解實數![]() 的最大值.
的最大值.
試題解析:
(1)當![]() 時,
時, ![]() ,
, ![]() .
.
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
∴![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .
.
(2)![]() ,
,
當![]() 時,由
時,由![]() ,知
,知![]() ,
,
所以, ![]() 在
在![]() 上是單調增函數,且圖象不間斷,
上是單調增函數,且圖象不間斷,
又![]() ,∴當
,∴當![]() 時,
時, ![]() ,
,
∴函數![]() 在區間
在區間![]() 上沒有零點,不合題意.
上沒有零點,不合題意.
當![]() 時,由
時,由![]() ,解得
,解得![]() ,
,
若![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上是單調減函數,
上是單調減函數,
若![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上是單調增函數,
上是單調增函數,
∴當![]() 時,
時, ![]() ,
,
又∵![]() ,
, ![]() 在
在![]() 上的圖象不間斷,
上的圖象不間斷,
∴函數![]() 在區間
在區間![]() 上有1個零點,符合題意.
上有1個零點,符合題意.
綜上所述, ![]() 的取值范圍為
的取值范圍為![]() .
.
(3)假設存在正整數![]() ,使得
,使得![]() 在
在![]() 上恒成立,
上恒成立,
則由![]() 知
知![]() ,從而
,從而![]() 對
對![]() 恒成立(*)
恒成立(*)
記![]() ,得
,得![]() ,
,
設![]() ,
, ![]() ,
,
∴![]() 在
在![]() 是單調增函數,
是單調增函數,
又![]() 在
在![]() 上圖象是不間斷的,
上圖象是不間斷的,
∴存在唯一的實數![]() ,使得
,使得![]() ,
,
∴當![]() 時,
時, ![]() 在
在![]() 上遞減,
上遞減,
當![]() 時,
時, ![]() 在
在![]() 上遞增,
上遞增,
∴當![]() 時,
時, ![]() 有極小值,即為最小值,
有極小值,即為最小值, ![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴ ![]() ,
,
由(*)知, ![]() ,又
,又![]() ,
, ![]() ,∴
,∴ ![]() 的最大值為3,
的最大值為3,
即存在最大的正整數![]() ,使得
,使得![]() 在
在![]() 上恒成立.
上恒成立.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某旅游點有50輛自行車供游客租賃使用,管理這些自行車的費用是每日115元.根據經驗,若每輛自行車的日租金不超過6元,則自行車可以全部租出;若超過6元,則每提高1元,租不出去的自行車就增加3輛.
規定:每輛自行車的日租金不超過20元,每輛自行車的日租金x元只取整數,并要求出租所有自行車一日的總收入必須超過一日的管理費用,用y表示出租所有自行車的日凈收入(即一日中出租所有自行車的總收入減去管理費后的所得).
(1)求函數y=f(x)的解析式及定義域;
(2)試問日凈收入最多時每輛自行車的日租金應定為多少元?日凈收入最多為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】AC為對稱軸的拋物線的一部分,點B到邊AC的距離為2km,另外兩邊AC,BC的長度分別為8km,2 ![]() km.現欲在此地塊內建一形狀為直角梯形DECF的科技園區.
km.現欲在此地塊內建一形狀為直角梯形DECF的科技園區. 
(1)求此曲邊三角形地塊的面積;
(2)求科技園區面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《城市規劃管理意見》里面提出“新建住宅要推廣街區制,原則上不再建設封閉住宅小區,已建成的封閉小區和單位大院要逐步打開”,這個消息在網上一石激起千層浪,各種說法不一而足.某網站為了解居民對“開放小區”認同與否,從![]() 歲的人群中隨機抽取了
歲的人群中隨機抽取了![]() 人進行問卷調查,并且做出了各個年齡段的頻率分布直方圖(部分)如圖所示,同時對
人進行問卷調查,并且做出了各個年齡段的頻率分布直方圖(部分)如圖所示,同時對![]() 人對這“開放小區”認同情況進行統計得到下表:
人對這“開放小區”認同情況進行統計得到下表:
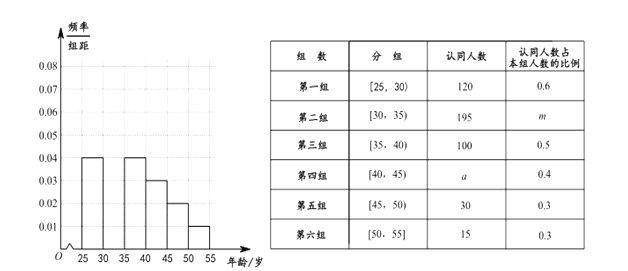
(Ⅰ)完成所給的頻率分布直方圖,并求![]() 的值;
的值;
(Ⅱ)如果從![]() 兩個年齡段中的“認同”人群中,按分層抽樣的方法抽取6人參與座談會,然后從這6人中隨機抽取2人作進一步調查,求這2人的年齡都在
兩個年齡段中的“認同”人群中,按分層抽樣的方法抽取6人參與座談會,然后從這6人中隨機抽取2人作進一步調查,求這2人的年齡都在![]() 內的概率 .
內的概率 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com