
���}Ŀ����֪�E�A ![]() ���x���ʞ�
���x���ʞ� ![]() �����^�c(di��n)
�����^�c(di��n) ![]()
������E�A ![]() �ķ��̣�
�ķ��̣�
�����O(sh��)ֱ�� ![]() �c�A
�c�A ![]() �������c(di��n)
�������c(di��n) ![]() ����
���� ![]() �c�E�A
�c�E�A ![]() ֻ��һ��(g��)�����c(di��n)
ֻ��һ��(g��)�����c(di��n) ![]() .
.
�����C�� ![]() ��
��
�ڮ�(d��ng) ![]() ���ֵ�r(sh��)��
���ֵ�r(sh��)�� ![]() ȡ�����ֵ����������ֵ.
ȡ�����ֵ����������ֵ.
���𰸡��⣺(I)�E�AE�ķ��̞� ![]()
������?y��n)�ֱ�� ![]() �c�AC:
�c�AC: ![]() ������A,��
������A,�� ![]() ,
,
�� ![]() ��
��
����?y��n)?![]() �c�E�AEֻ��һ��(g��)�����c(di��n)B ��
�c�E�AEֻ��һ��(g��)�����c(di��n)B ��
�� 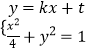 ��
�� ![]() ,�Ҵ˷�����Ψһ��.
,�Ҵ˷�����Ψһ��.
�t ![]() ��
�� ![]()
���ɢ٢�,�� ![]()
���O(sh��) ![]() ����
���� ![]() ��
�� ![]()
���f�_(d��)����, ![]()
�� ![]() �c(di��n)�ڙE�A��,��
�c(di��n)�ڙE�A��,�� ![]()
�� ![]()
��ֱ��������OAB��, ![]()
![]()
�� ![]()
����������1������(j��)�E�A�����|(zh��)�õ�![]() ��
��![]() ���ٌ��c(di��n)��
���ٌ��c(di��n)��![]() ��2������E�A���̣��ⷽ�̽M���ɵõ���
��2������E�A���̣��ⷽ�̽M���ɵõ���
��2���ٸ���(j��)ֱ���c�A��λ���P(gu��n)ϵ�������c(di��n)��ֱ���ľ��x��ʽ���Եõ�t��k��R�ĵ����P(gu��n)ϵ���ٸ���(j��)ֱ���c�E�A�Ľ��c(di��n)��һ��(g��)��(li��n)�����̣��ɵ�![]() =0���Y(ji��)�σɂ�(g��)��ʽ����ȥt2���ɵõ���
=0���Y(ji��)�σɂ�(g��)��ʽ����ȥt2���ɵõ���
����?y��n)?/span>![]() ��ֱ�������Σ��ʸ���(j��)���ɶ����ɵ�
��ֱ�������Σ��ʸ���(j��)���ɶ����ɵ�![]() ,��OA�L(zh��ng)��R����Ҫ��B�c(di��n)����(bi��o)��R��ʾ�����������ʽ���ɵõ�AB���L(zh��ng)�ȡ�
,��OA�L(zh��ng)��R����Ҫ��B�c(di��n)����(bi��o)��R��ʾ�����������ʽ���ɵõ�AB���L(zh��ng)�ȡ�



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����ݽy(t��ng)Ӌ(j��)�־�ij�ؾ�����������{(di��o)����![]() �ˣ�������(j��)���Ô�(sh��)��(j��)���˘ӱ����l�ʷ�
�ˣ�������(j��)���Ô�(sh��)��(j��)���˘ӱ����l�ʷ�
��ֱ���D��ÿ��(g��)�ֽM��������c(di��n)���������Ҷ��c(di��n)�����һ�M��ʾ������![]() ����
����

��1���������������![]() ���l�ʣ�
���l�ʣ�
��2������(j��)�l�ʷֲ�ֱ���D����ӱ���(sh��)��(j��)����λ��(sh��)��
��3�����˷�������������c���g���I(y��)�ȷ�����P(gu��n)ϵ����횰���������?g��u)��@![]() ���зӳ�ӷ������
���зӳ�ӷ������![]() �����M(j��n)һ���������t��������
�����M(j��n)һ���������t��������![]() ���@�Α�(y��ng)������ˣ�
���@�Α�(y��ng)������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)��ABC�ă�(n��i)��A,B,C����(du��)��߅�քe��a,b,c����֪A���g�ǣ���2a ![]() ����
���� ![]() ���t��ABC����e�����ֵ�� .
���t��ABC����e�����ֵ�� .
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�ڡ�ABC�У���A��B��C����(du��)��߅�քe��a��b��c����a��b��c�ɵȱȔ�(sh��)�У�c= ![]() bsinC��ccosB��
bsinC��ccosB��
������B�Ĵ�С��
������b=2 ![]() �����ABC�����L(zh��ng)����e��
�����ABC�����L(zh��ng)����e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���c(di��n)![]() ��A�ĵĈA�^�c(di��n)
��A�ĵĈA�^�c(di��n)![]() ��
��![]() ������
������![]() �Ĵ�ֱƽ�־����A
�Ĵ�ֱƽ�־����A![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ����
����![]() ,
,
��1����ֱ��![]() �ķ��̣� ��2����A
�ķ��̣� ��2����A![]() �ķ��̡�
�ķ��̡�
��3���O(sh��)�c(di��n)![]() �ڈA
�ڈA![]() �ϣ�ԇ̽��ʹ
�ϣ�ԇ̽��ʹ![]() ����e�� 8 ���c(di��n)
����e�� 8 ���c(di��n)![]() ���Ўׂ�(g��)���C����ĽY(ji��)Փ
���Ўׂ�(g��)���C����ĽY(ji��)Փ
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
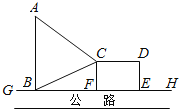
���}Ŀ����D��![]() �ǖ|������Ĺ�·����(c��)��߅������ij��˾��(zh��n)����
�ǖ|������Ĺ�·����(c��)��߅������ij��˾��(zh��n)����![]() �ϵ�һ�c(di��n)
�ϵ�һ�c(di��n)![]() �����������
�����������![]() ̎��һ�}(c��ng)��(k��)�����ڹ�·ͬ��(c��)����һ��(g��)�����Οo����D(zhu��n)վ
̎��һ�}(c��ng)��(k��)�����ڹ�·ͬ��(c��)����һ��(g��)�����Οo����D(zhu��n)վ![]() ������߅
������߅![]() ��
��![]() �ϣ����F(xi��n)�Ă}(c��ng)��(k��)
�ϣ����F(xi��n)�Ă}(c��ng)��(k��)![]() ��
��![]() �����D(zhu��n)վ�քe�ރɗl��·
�����D(zhu��n)վ�քe�ރɗl��·![]() ��
��![]() ����֪
����֪![]() ����
����![]() ���O(sh��)
���O(sh��)![]() ��
��![]() ��
��
��1����![]() �P(gu��n)��
�P(gu��n)��![]() �ĺ���(sh��)����ʽ��
�ĺ���(sh��)����ʽ��
��2��������D(zhu��n)վ���܇����������������L(zh��ng)����r(ji��)��![]() �fԪ
�fԪ![]() ���ɗl��·��r(ji��)��
���ɗl��·��r(ji��)��![]() �fԪ
�fԪ![]() ������
������![]() ȡ��ֵ�r(sh��)��ԓ��˾�����D(zhu��n)�����̓ɗl��·����r(ji��)
ȡ��ֵ�r(sh��)��ԓ��˾�����D(zhu��n)�����̓ɗl��·����r(ji��)![]() ��ͣ�
��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�AC�� ![]() +
+ ![]() =1��a��b��0�����x���ʞ�
=1��a��b��0�����x���ʞ� ![]() ���c(di��n)B�ǙE�AC������c(di��n)���c(di��n)Q�ڙE�AC�ϣ�����B�c(di��n)����
���c(di��n)B�ǙE�AC������c(di��n)���c(di��n)Q�ڙE�AC�ϣ�����B�c(di��n)����
�������E�AV�^�c(di��n)���� ![]() ��
�� ![]() ������E�AC�ķ��̣�
������E�AC�ķ��̣�
������ֱ��l��y=kx+b�c�E�AC����B��P���c(di��n)������PQ��ֱ���ĈA�^�c(di��n)B���C��������k��R�� ![]() =
= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����������g(sh��)�����҇�(gu��)�Ŵ���(n��i)�ݘO���S���Ĕ�(sh��)�W(xu��)�����������ᵽ��һ�N���顰�c�����������w����D���� ![]() ����Σ���
����Σ��� ![]() .���ˎ��w�У�
.���ˎ��w�У� ![]() ��
�� ![]() ��
�� ![]() ����߅�L(zh��ng)��
����߅�L(zh��ng)�� ![]() �ĵ�߅�����Σ��t�ˎ��w�ı���e�飨 ��
�ĵ�߅�����Σ��t�ˎ��w�ı���e�飨 ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A ![]() ���x���ʞ�
���x���ʞ� ![]() �����^�c(di��n)
�����^�c(di��n) ![]() .
.
��1����E�A ![]() �ķ��̣�
�ķ��̣�
��2���O(sh��)���^ԭ�c(di��n) ![]() ��ֱ��
��ֱ�� ![]() �c�E�A
�c�E�A ![]() ����
���� ![]() ���c(di��n)��ֱ��
���c(di��n)��ֱ�� ![]() ��б�ʷքe��
��б�ʷքe�� ![]() ���M��
���M�� ![]() ��ԇ������(d��ng)
��ԇ������(d��ng) ![]() ׃���r(sh��)��
׃���r(sh��)�� ![]() �Ƿ�鶨ֵ�����ǣ�����˶�ֵ�����C����ĽY(ji��)Փ�������ǣ�Ո(q��ng)�f������.
�Ƿ�鶨ֵ�����ǣ�����˶�ֵ�����C����ĽY(ji��)Փ�������ǣ�Ո(q��ng)�f������.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com