
【題目】潮州統計局就某地居民的月收入調查了![]() 人,并根據所得數據畫了樣本的頻率分
人,并根據所得數據畫了樣本的頻率分
布直方圖(每個分組包括左端點,不包括右端點,如第一組表示收入在![]() )。
)。

(1)求居民月收入在![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析居民的收入與年齡、職業等方面的關系,必須按月收入再從這![]() 人中分層抽樣方法抽出
人中分層抽樣方法抽出![]() 人作進一步分析,則月收入在
人作進一步分析,則月收入在![]() 的這段應抽多少人?
的這段應抽多少人?
【答案】(1)0.15;(2)2400;(3)25.
【解析】試題分析:(1)根據頻率=小矩形的高×組距來求;(2)根據中位數的左右兩邊的矩形的面積和相等,所以只需求出從左開始面積和等于0.5的底邊橫坐標的值即可,運用取中間數乘頻率,再求之和,計算可得平均數;(3)求出月收入在[2500,3000)的人數,用分層抽樣的抽取比例乘以人數,可得答案.
試題解析:
(1)月收入在![]() 的頻率為
的頻率為![]() ;
;
(2)從左數第一組的頻率為![]() ;
;
第二組的頻率為![]() ;
;
第三組的頻率為![]() ;
;
∴中位數在第三組,設中位數為![]()
則![]()
得![]()
∴中位數為2400(元)
由![]()
樣本的平均數為2400(元)
(3)月收入在![]() 的頻數為
的頻數為![]() (人),
(人),
∵抽取的樣本容量為100,∴抽取的比例為![]() ,
,
∴月收入在![]() 的這段應抽取為
的這段應抽取為![]() (人)
(人)


 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:
【題目】農科院的專家為了了解新培育的甲、乙兩種麥苗的長勢情況,從甲、乙兩種麥苗的試驗田中各抽取6株麥苗測量麥苗的株高,數據如下:(單位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在給出的方框內繪出所抽取的甲、乙兩種麥苗株高的莖葉圖;
(2)分別計算所抽取的甲、乙兩種麥苗株高的平均數與方差,并由此判斷甲、乙兩種麥苗的長勢情況.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是某校高三一次月考5個班級的數學、物理的平均成績:
班級 | 1 | 2 | 3 | 4 | 5 |
數學( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般來說,學生的物理成績與數學成績具有線性相關關系,根據上表提供的數據,求兩個變量![]() ,
, ![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅱ)從以上5個班級中任選兩個參加某項活動,設選出的兩個班級中數學平均分在115分以上的個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:  ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店銷售剛剛上市的某知名品牌的高三數學單元卷,按事先擬定的價格進行5天試銷,每種單價試銷1天,得到如下數據:
單價 | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
(1)求試銷5天的銷量的方差和![]() 對
對![]() 的回歸直線方程;
的回歸直線方程;
(2)預計今后的銷售中,銷量與單價服從(1)中的回歸方程,已知每冊單元卷的成本是14元,為了獲得最大利潤,該單元卷的單價卷的單價應定為多少元?
(附: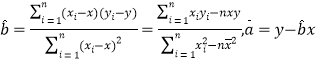 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是某校高三一次月考5個班級的數學、物理的平均成績:
班級 | 1 | 2 | 3 | 4 | 5 |
數學( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般來說,學生的物理成績與數學成績具有線性相關關系,根據上表提供的數據,求兩個變量![]() ,
, ![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅱ)從以上5個班級中任選兩個參加某項活動,設選出的兩個班級中數學平均分在115分以上的個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:  ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答
(1)在區間[1,3]上任取兩整數a、b,求二次方程x2+2ax+b2=0有實數根的概率.
(2)在區間[1,3]上任取兩實數a、b,求二次方程x2+2ax+b2=0有實數根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在高中學習過程中,同學們經常這樣說:“如果物理成績好,那么學習數學就沒什么問題.”某班針對“高中生物理學習對數學學習的影響”進行研究,得到了學生的物理成績與數學成績具有線性相關關系的結論.現從該班隨機抽取5名學生在一次考試中的物理和數學成績,如下表:
編號 成績 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
數學( | 130 | 125 | 110 | 95 | 90 |
(1)求數學成績![]() 關于物理成績
關于物理成績![]() 的線性回歸方程
的線性回歸方程![]() (
(![]() 精確到
精確到![]() ),若某位學生的物理成績為80分,預測他的數學成績;
),若某位學生的物理成績為80分,預測他的數學成績;
(2)要從抽取的五位學生中隨機選出三位參加一項知識競賽,以![]() 表示選中的學生的數學成績高于100分的人數,求隨機變量
表示選中的學生的數學成績高于100分的人數,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
(參數公式: 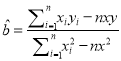 ,
, ![]() .)
.)
參考數據: ![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
, ![]() .
.
(1)當n=1,2,3時,分別比較f(n)與g(n)的大小(直接給出結論);
(2)由(1)猜想f(n)與g(n)的大小關系,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com