
【題目】已知定義域為R的函數f(x)= ![]() 是奇函數.
是奇函數.
(1)求f(x)的解析式;
(2)若對任意t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范圍.
【答案】
(1)解:因為f(x)是定義在R上的奇函數,
所以f(0)=0,
所以f(0)= ![]() =0,所以b=1,
=0,所以b=1,
因為f(x)= ![]() ,
,
所以f(﹣x)= ![]() =
= ![]() .
.
因為f(﹣x)=﹣f(x),
所以 ![]() =
= ![]() ,
,
所以(2﹣a)(1﹣2x)=0,
所以a=2,
所以f(x)= ![]()
(2)解:因為f(t2﹣2t)+f(2t2﹣k)<0恒成立,
所以f(t2﹣2t)<﹣f(2t2﹣k)恒成立,
因為f(x)為R上的奇函數,
所以f(t2﹣2t)<f(﹣2t2+k)恒成立,
因為函數f(x)在R上單調遞減,
所以t2﹣2t>﹣2t2+k恒成立,所以k<3t2﹣2t恒成立,
又因為g(t)=3t2﹣2t在R上最小值為 ![]()
k<﹣ ![]()
【解析】(1)在R上的奇函數,f(0)=0求參數;(2)不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,轉化為k<(3t2﹣2t)min求解.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知袋中放有形狀大小相同的小球若干,其中標號為0的小球1個,標號為1的小球1個,標號為2的小球![]() 個,從袋中隨機抽取一個小球,取到標號為2的小球的概率為
個,從袋中隨機抽取一個小球,取到標號為2的小球的概率為![]() ,現從袋中不放回地隨機取出2個小球,記第一次取出的小球標號為
,現從袋中不放回地隨機取出2個小球,記第一次取出的小球標號為![]() ,第二次取出的小球標號為
,第二次取出的小球標號為![]() .
.
(1)記“![]() ”為事件
”為事件![]() ,求事件
,求事件![]() 發生的概率.
發生的概率.
(2)在區間![]() 上任取兩個實數
上任取兩個實數![]() ,求事件
,求事件![]() “
“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為豐富人民群眾業余生活,某市擬建設一座江濱公園,通過專家評審篩選處建設方案A和B向社會公開征集意見,有關部分用簡單隨機抽樣方法調查了500名市民對這兩種方案的看法,結果用條形圖表示如下:
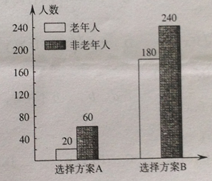
(1)根據已知條件完成下面![]() 列聯表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過
列聯表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過![]() 的前提下認為是否選擇方案A和年齡段有關?
的前提下認為是否選擇方案A和年齡段有關?
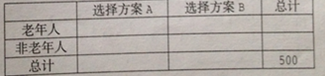
(2)根據(1)的結論,能否提出一個更高的調查方法,使得調查結果更具代表性,說明理由.
附:

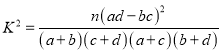
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的焦點在
的焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,拋物線
,拋物線![]() 的焦點在
的焦點在![]() 軸上,
軸上, ![]() 的中心和
的中心和![]() 的頂點均為原點,點
的頂點均為原點,點 在
在![]() 上,點
上,點![]() 在
在![]() 上,
上,
(1)求曲線![]() ,
, ![]() 的標準方程;
的標準方程;
(2)請問是否存在過拋物線![]() 的焦點
的焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() ,使得以線段
,使得以線段![]() 為直徑的圓過原點
為直徑的圓過原點![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】太極圖是由黑白兩個魚形紋組成的圖案,俗稱陰陽魚,太極圖展現了一種相互轉化,相互統一的和諧美.定義:能夠將圓![]() 的周長和面積同時等分成兩部分的函數稱為圓
的周長和面積同時等分成兩部分的函數稱為圓![]() 的一個“太極函數”.下列有關說法中:
的一個“太極函數”.下列有關說法中:

①對圓![]() 的所有非常數函數的太極函數中,一定不能為偶函數;
的所有非常數函數的太極函數中,一定不能為偶函數;
②函數![]() 是圓
是圓![]() 的一個太極函數;
的一個太極函數;
③存在圓![]() ,使得
,使得![]() 是圓
是圓![]() 的太極函數;
的太極函數;
④直線![]() 所對應的函數一定是圓
所對應的函數一定是圓![]() 的太極函數.
的太極函數.
所有正確說法的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() )將
)將![]() 的圖象向右平移兩個單位,得到函數
的圖象向右平移兩個單位,得到函數![]() 的圖象.
的圖象.
(1)求函數![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且僅有一個實根,求
上有且僅有一個實根,求![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 與
與![]() 的圖像關于直線
的圖像關于直線![]() 對稱,設
對稱,設![]() ,已知
,已知![]() 對任意的
對任意的![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的方程x2+ax+a﹣2=0.
(1)當該方程的一個根為1時,求a的值及該方程的另一根;
(2)求證:不論a取何實數,該方程都有兩個不相等的實數根.
(3)設該方程的兩個實數根分別為x1 , x2 , 若2(x1+x2)+x1x2+10=0,求a的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com