
【題目】2020年是我國全面建成小康社會和“十三五”規劃收官之年,也是佛山在經濟總量超萬億元新起點上開啟發展新征程的重要歷史節點.作為制造業城市,佛山一直堅持把創新擺在制造業發展全局的前置位置和核心位置,聚焦打造成為面向全球的國家制造業創新中心,走“世界科技+佛山智造+全球市場”的創新發展之路.在推動制造業高質量發展的大環境下,佛山市某工廠統籌各類資源,進行了積極的改革探索.下表是該工廠每月生產的一種核心產品的產量![]() (件)與相應的生產總成本
(件)與相應的生產總成本![]() (萬元)的四組對照數據.
(萬元)的四組對照數據.
| 5 | 7 | 9 | 11 |
| 200 | 298 | 431 | 609 |
工廠研究人員建立了![]() 與
與![]() 的兩種回歸模型,利用計算機算得近似結果如下:
的兩種回歸模型,利用計算機算得近似結果如下:
模型①:![]() ;
;
模型②:![]() .
.
其中模型①的殘差(實際值預報值)圖如圖所示:
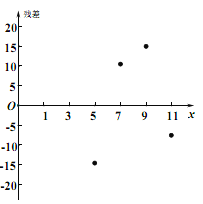
(1)根據殘差分析,判斷哪一個更適宜作為![]() 關于
關于![]() 的回歸方程?并說明理由;
的回歸方程?并說明理由;
(2)市場前景風云變幻,研究人員統計了20個月的產品銷售單價,得到頻數分布表如下:
銷售單價分組(萬元) |
|
|
|
頻數 | 10 | 6 | 4 |
若以這20個月銷售單價的平均值定為今后的銷售單價(同一組中的數據用該組區間的中點值作代表),結合你對(1)的判斷,當月產量為12件時,預測當月的利潤.
【答案】(1)模型①更適宜作為![]() 關于
關于![]() 的回歸方程,見解析(2)295萬元.
的回歸方程,見解析(2)295萬元.
【解析】
(1) 模型①更適合作為y關于x的回歸方程.先根據模型②: y=68x- 160逐一算出四組數據的殘差, 并整理成表,再作出殘差圖,然后對比模型①與②,從殘差的絕對值大小、殘差點分布的帶狀區域的寬窄或殘差點離x軸的遠近進行理由闡述即可;
(2)先根據頻數分布表算出這20個月銷售單價的平均值,設月利潤為![]() 萬元,則
萬元,則![]() ,再把x=12代入,求出z的值即可得解.
,再把x=12代入,求出z的值即可得解.
(1)模型②的殘差數據如下表:
| 5 | 7 | 9 | 11 |
| 200 | 298 | 431 | 609 |
| 20 | -18 | -21 | 21 |
模型②的殘點圖如圖所示.
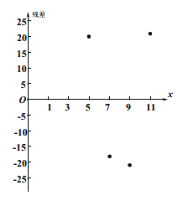
模型①更適宜作為![]() 關于
關于![]() 的回歸方程,因為:
的回歸方程,因為:
理由1:模型①這個4個樣本點的殘差的絕對值都比模型②的小.
理由2:模型①這4個樣本的殘差點落在的帶狀區域比模型②的帶狀區域更窄.
理由3:模型①這4個樣本的殘差點比模型②的殘差點更貼近![]() 軸.
軸.
(2)這20個月銷售單價的平均值為![]() ,
,
設月利潤為![]() 萬元,由題意知
萬元,由題意知![]() ,
,
當![]() 時,
時,![]() (萬元),
(萬元),
所以當月產量為12件時,預測當月的利潤為295萬元.


科目:高中數學 來源: 題型:
【題目】已知⊙M過點![]() ,且與⊙N:
,且與⊙N:![]() 內切,設⊙M的圓心M的軌跡為曲線C.
內切,設⊙M的圓心M的軌跡為曲線C.
(1)求曲線C的方程:
(2)設直線l不經過點![]() 且與曲線C相交于P,Q兩點.若直線PB與直線QB的斜率之積為
且與曲線C相交于P,Q兩點.若直線PB與直線QB的斜率之積為![]() ,判斷直線l是否過定點,若過定點,求出此定點坐標;若不過定點,請說明理由.
,判斷直線l是否過定點,若過定點,求出此定點坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,
, ![]()
(1)若![]() ,且
,且![]() 在其定義域上存在單調遞減區間,求實數
在其定義域上存在單調遞減區間,求實數![]() 的取值范圍;
的取值范圍;
(2)設函數![]() ,
, ![]() ,若
,若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)設函數![]() 的圖象
的圖象![]() 與函數
與函數![]() 的圖象
的圖象![]() 交于點
交于點![]() 、
、![]() ,過線段
,過線段![]() 的中點作
的中點作![]() 軸的垂線分別交
軸的垂線分別交![]() ,
, ![]() 于點
于點![]() 、
、![]() ,證明:
,證明: ![]() 在點
在點![]() 處的切線與
處的切線與![]() 在點
在點![]() 處的切線不平行.
處的切線不平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】港珠澳大橋是一座具有劃時代意義的大橋.它連通了珠海香港澳門三地,大大縮短了三地的時空距離,盤活了珠江三角洲的經濟,被譽為新的世界七大奇跡.截至2019年10月23日8點,珠海公路口岸共驗放出入境旅客超過1400萬人次,日均客流量已經達到4萬人次,驗放出入境車輛超過70萬輛次,2019年春節期間,客流再次大幅增長,日均客流達8萬人次,單日客流量更是創下11.3萬人次的最高紀錄.
2019年從五月一日開始的連續100天客流量頻率分布直方圖如下
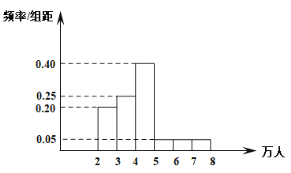
(1)①同一組數據用該區間的中點值代替,根據頻率分布直方圖.估計客流量的平均數.
②求客流量的中位數.
(2)設這100天中客流量超過5萬人次的有![]() 天,從這
天,從這![]() 天中任取兩天,設
天中任取兩天,設![]() 為這兩天中客流量超過7萬人的天數.求
為這兩天中客流量超過7萬人的天數.求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,圓![]() 的參數方程為
的參數方程為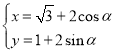 (
(![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸的正半軸為極軸建立極坐標系,且長度單位相同.
軸的正半軸為極軸建立極坐標系,且長度單位相同.
(1)求圓![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() :
:![]() (
(![]() 為參數)被圓
為參數)被圓![]() 截得的弦長為2,求直線
截得的弦長為2,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com