
【題目】如圖是根據某班50名同學在某次數學測驗中的成績(百分制)繪制的概率分布直方圖,其中成績分組區間為:[40,50),[50,60),…,[80,90),[90,100]. 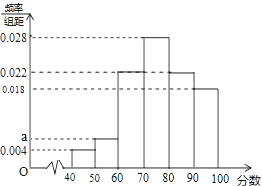
(1)求圖中a的值;
(2)計算該班本次的數學測驗成績不低于80分的學生的人數;
(3)根據頻率分布直方圖,估計該班本次數學測驗成績的平均數與中位數(要求中位數的估計值精確到0.1)
【答案】
(1)解:頻率分布直方圖,所有小矩形的面積之和為1,由此得
(0.004+a+0.022+0.028+0.022+0.018)×10=1
解得a=0.006
(2)解:該班本次的數學測驗成績不低于80分學生的人數為
50×(0.022×10+0.018×10)=20
(3)解:該班本次數學測驗成績的平均數的估計值為
0.04×45+0.06×55+0.22×65+0.28×75+0.22×85+0.18×95=76.2
前三個區間的頻率之和為0.04+0.06+0.22=0.32<0.5,前四個區間的頻率之和為
0.04+0.06+0.22+0.28=0.6>0.5,所以該班本次數學測驗成績的中位數在70于80之間.
該班本次數學測驗成績的中位數的估計值為70+ ![]() ×10≈76.4
×10≈76.4
【解析】(1)根據頻率分布直方圖,所有小矩形的面積之和為1,即可求出a的值,(2)先求出成績不低于80分的學生的頻率,即可求出相對應的人數,(3)根據平均數和中位數的定義即可計算.
【考點精析】本題主要考查了頻率分布直方圖和平均數、中位數、眾數的相關知識點,需要掌握頻率分布表和頻率分布直方圖,是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式,可展示數據的分布情況.通過作圖既可以從數據中提取信息,又可以利用圖形傳遞信息;⑴平均數、眾數和中位數都是描述一組數據集中趨勢的量;⑵平均數、眾數和中位數都有單位;⑶平均數反映一組數據的平均水平,與這組數據中的每個數都有關系,所以最為重要,應用最廣;⑷中位數不受個別偏大或偏小數據的影響;⑸眾數與各組數據出現的頻數有關,不受個別數據的影響,有時是我們最為關心的數據才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】如圖,D是直角△ABC斜邊BC上一點,AC= ![]() DC.
DC. 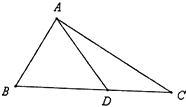
(Ⅰ)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD= ![]() ,求DC的長.
,求DC的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】兩個非零向量 ![]() 、
、 ![]() 不共線.
不共線.
(1)若 ![]() =
= ![]() +
+ ![]() ,
, ![]() =2
=2 ![]() +8
+8 ![]() ,
, ![]() =3(
=3( ![]() ﹣
﹣ ![]() ),求證:A、B、D三點共線;
),求證:A、B、D三點共線;
(2)求實數k使k ![]() +
+ ![]() 與2
與2 ![]() +k
+k ![]() 共線.
共線.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《孫子算經》是中國古代重要的數學著作,約成書于四、五世紀,也就是大約一千五百年前,傳本的《孫子算經》共三卷,卷中有一問題:“今有方物一束,外周一匝有三十二枚,問積幾何?”該著作中提出了一種解決問題的方法:“重置二位,左位減八,余加右位,至盡虛加一,即得.”通過對該題的研究發現,若一束方物外周一匝的枚數![]() 是8的整數倍時,均可采用此方法求解,如圖,是解決這類問題的程序框圖,若輸入
是8的整數倍時,均可采用此方法求解,如圖,是解決這類問題的程序框圖,若輸入![]() ,則輸出的結果為( )
,則輸出的結果為( )
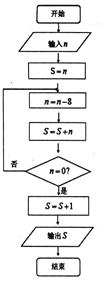
A. 120 B. 121 C. 112 D. 113
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐P﹣ABCD的底面為直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中點. 
(1)證明:面PAD⊥面PCD;
(2)求直線AC與PB所成角的余弦值;
(3)求二面角A﹣MC﹣B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)對任意實數x,y滿足f(x)+f(y)=f(x+y)+3,f(3)=6,當x>0 時,f(x)>3,那么,當f(2a+1)<5時,實數a的取值范圍是
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直線![]() 與
與![]() 相交于
相交于![]() 兩點,且滿足:①
兩點,且滿足:①![]() 與
與![]() (
(![]() 為坐標原點)的斜率之和為2;②直線
為坐標原點)的斜率之和為2;②直線![]() 與圓
與圓![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com