
【題目】已知圓![]() 的方程為:
的方程為: ![]() 。
。
(1)求圓![]() 的圓心所在直線方程一般式;
的圓心所在直線方程一般式;
(2)若直線![]() 被圓
被圓![]() 截得弦長為
截得弦長為![]() ,試求實數
,試求實數![]() 的值;
的值;
(3)已知定點![]() ,且點
,且點![]() 是圓
是圓![]() 上兩動點,當
上兩動點,當![]() 可取得最大值為
可取得最大值為![]() 時,求滿足條件的實數
時,求滿足條件的實數![]() 的值。
的值。
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】試題分析:
(1)配方得圓的標準方程,可得圓心坐標滿足![]() ,消去
,消去![]() 可得圓心所在直線方程;
可得圓心所在直線方程;
(2)由弦長、半徑結合勾股定理求出圓心到直線的距離,再由點到直線距離公式求得圓心到直線的距離,兩者相等可解得m;
(3)本題關鍵是∠APB何時最大?由于P點固定,因此當PA,PB是圓的兩切線時∠APB最大,由此角是90°,這樣PACB是正方形,可得CP=![]() ,由兩點間距離公式可求得m.
,由兩點間距離公式可求得m.
試題解析:
(1)由已知圓C的方程為: ![]()
所以圓心為![]()
所以圓心在直線方程為![]()
(2)由已知r=2,又弦長為![]() ,
,
所以圓心到直線距離為![]()
所以![]()
解得m=-1或m=![]() 3
3
(3)當PA、PB為圓的兩條切線時,∠APB取最大值.
此時∠APB=90°,又CA⊥PA,CB⊥PB,CA=CB
所以四邊形PACB為正方形,則∣CP∣=![]()
即P到圓心C的距離=![]()
解得![]()


 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案 周周清檢測系列答案
周周清檢測系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)用“五點法”在如圖所示的虛線方框內作出函數![]() 在一個周期內的簡圖(要求:列表與描點,建立直角坐標系);
在一個周期內的簡圖(要求:列表與描點,建立直角坐標系);

(2)函數![]() 的圖像可以通過函數
的圖像可以通過函數![]() 的圖像經過“先伸縮后平移”的規則變換而得到,請寫出一個這樣的變換!
的圖像經過“先伸縮后平移”的規則變換而得到,請寫出一個這樣的變換!
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cos(![]() +x)cos(
+x)cos(![]() -x),g(x)=
-x),g(x)=![]() sin 2x-
sin 2x-![]() .
.
(1)求函數f(x)的最小正周期;
(2)求函數h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD是梯形,四邊形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE= ![]() CD=2,M是線段AE上的動點.
CD=2,M是線段AE上的動點. 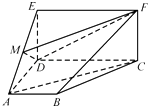
(Ⅰ)試確定點M的位置,使AC∥平面MDF,并說明理由;
(Ⅱ)在(Ⅰ)的條件下,求平面MDF將幾何體ADE﹣BCF分成的兩部分的體積之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知線段![]() 的端點
的端點![]() ,端點
,端點![]() 在圓
在圓![]() 上運動
上運動
(Ⅰ)求線段![]() 的中點
的中點![]() 的軌跡方程.
的軌跡方程.
(Ⅱ) 設動直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,問在
兩點,問在![]() 軸正半軸上是否存在定點
軸正半軸上是否存在定點![]() ,使得直線
,使得直線![]() 與直線
與直線![]() 關于
關于![]() 軸對稱?若存在,請求出點
軸對稱?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查喜歡旅游是否與性別有關,調查人員就“是否喜歡旅游”這個問題,在火車站分別隨機調研了50名女性和50名男性,根據調研結果得到如圖所示的等高條形圖
(1)完成下列2×2列聯表:
喜歡旅游 | 不喜歡旅游 | 合計 | |
女性 | |||
男性 | |||
合計 |
(2)能否在犯錯率不超過0.025的前提下認為“喜歡旅游與性別有關” 附:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)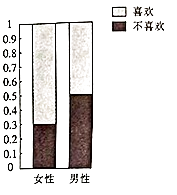
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數![]() .
.
(Ⅰ)當![]() 時,解不等式
時,解不等式![]() ;
;
(Ⅱ)若關于![]() 的方程
的方程![]() 的解集中恰有一個元素,求
的解集中恰有一個元素,求![]() 的取值范圍;
的取值范圍;
(Ⅲ)設![]() ,若對任意
,若對任意![]() ,函數
,函數![]() 在區間
在區間![]() 上的最大值與最小值的和不大于
上的最大值與最小值的和不大于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com