
【題目】甲、乙兩位學生參加數學競賽培訓,在培訓期間,他們參加的5次預賽成績記錄如下:
甲 | 82 | 82 | 79 | 95 | 87 |
乙 | 95 | 75 | 80 | 90 | 85 |
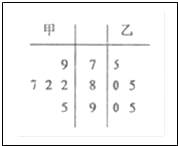
(1)請用莖葉圖表示這兩組數據;
(2)從甲、乙兩人的成績中各隨機抽取一個,求甲的成績比乙高的概率;
(3)現要從中選派一人參加9月份的全國數學聯賽,從統計學的角度考慮,你認為選派哪位學生參加合適?請說明理由.
【答案】
(1)解:作出莖葉圖如下圖
(2)解:記甲被抽到的成績為x,乙被抽到成績為y,用數對(x,y)表示基本事件:
(82,95),(82,75),(82,80),(82,90),(82,85),
(82,95),(82,75),(82,80),(82,90),(82,85),
(79,95),(79,75),(79,80),(79,90),(79,85),
(95,95),(95,75),(95,80),(95,90),(95,85),
(87,95),(87,75),(87,80),(87,90),(87,85),
基本事件總數n=25
記“甲的成績比乙高”為事件A,事件A包含的基本事件:
(82,75),(82,80),(82,75),(82,80),(79,75),(95,75),
(95,80),(95,90),(95,85),(87,75),(87,80),(87,85),
事件A包含的基本事件數m=12
所以 ![]()
(3)解:派甲參賽比較合適,理由如下: ![]() =
= ![]() (70×1+80×3+90×1+9+2+2+7+5)=85,
(70×1+80×3+90×1+9+2+2+7+5)=85,
![]() =
= ![]() (70×1+80×2+90×2+5+0+5+0+5)=85
(70×1+80×2+90×2+5+0+5+0+5)=85
![]()
![]()
∵ ![]() =
= ![]() ,S甲2<S乙2∴甲的成績較穩定,派甲參賽比較合適
,S甲2<S乙2∴甲的成績較穩定,派甲參賽比較合適
【解析】(1)用莖葉圖表示兩組數據,首先要先確定“莖”值,再將數據按“莖”值分組分類表示在“葉”的位置.(2)要從甲、乙兩人的成績中各隨機抽取一個,求甲的成績比乙高的概率,首先要計算“要從甲、乙兩人的成績中各隨機抽取一個”的事件個數,再計算“甲的成績比乙高”的事件個數,代入古典概型公式即可求解.(3)選派學生參加大型比賽,是要尋找成績發揮比較穩定的優秀學生,所以要先分析兩名學生的平均成績,若平均成績相等,再由莖葉圖分析出成績相比穩定的學生參加.
【考點精析】本題主要考查了莖葉圖和極差、方差與標準差的相關知識點,需要掌握莖葉圖又稱“枝葉圖”,它的思路是將數組中的數按位數進行比較,將數的大小基本不變或變化不大的位作為一個主干(莖),將變化大的位的數作為分枝(葉),列在主干的后面,這樣就可以清楚地看到每個主干后面的幾個數,每個數具體是多少;標準差和方差越大,數據的離散程度越大;標準差和方程為0時,樣本各數據全相等,數據沒有離散性;方差與原始數據單位不同,解決實際問題時,多采用標準差才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】某校高二年級學生會有理科生4名,其中3名男同學;文科生3名,其中有1名男同學.從這7名成員中隨機抽4人參加高中示范校驗收活動問卷調查.
(Ⅰ)設![]() 為事件“選出的4人中既有文科生又有理科生”,求事件
為事件“選出的4人中既有文科生又有理科生”,求事件![]() 的概率;
的概率;
(Ⅱ)設![]() 為選出的4人中男生人數與女生人數差的絕對值,求隨機變量
為選出的4人中男生人數與女生人數差的絕對值,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,平面ABCD⊥平面ADEF,四邊形ABCD為菱形,四邊形ADEF為矩形,M、N分別是EF、BC的中點,AB=2AF=2,∠CBA=60°.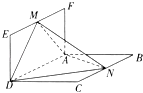
(1)求證:AN⊥DM;
(2)求直線MN與平面ADEF所成的角的正切值;
(3)求三棱錐D﹣MAN的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系 ![]() 中,以原點
中,以原點 ![]() 為極點,以
為極點,以 ![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線 ![]() 的極坐標方程為
的極坐標方程為 ![]() ,曲線
,曲線 ![]() 的參數方程為
的參數方程為 ![]() .
.
(1)求曲線 ![]() 的直角坐標方程與曲線
的直角坐標方程與曲線 ![]() 的普通方程;
的普通方程;
(2)試判斷曲線 ![]() 與
與 ![]() 是否存在兩個交點?若存在,求出兩交點間的距離;若不存在,說明理由.
是否存在兩個交點?若存在,求出兩交點間的距離;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4—4:坐標系與參數方程
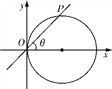
(Ⅰ)如圖,以過原點的直線的傾斜角θ為參數,求圓x2+y2-x=0的參數方程;
(Ⅱ)在平面直角坐標系中,已知直線l的參數方程為![]() (s為參數),曲線C的參數方程為
(s為參數),曲線C的參數方程為![]() (t為參數),若l與C相交于A,B兩點,求AB的長.
(t為參數),若l與C相交于A,B兩點,求AB的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系 ![]() 中,曲線
中,曲線 ![]() 的參數方程為
的參數方程為 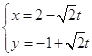 (
( ![]() 為參數),以原點
為參數),以原點 ![]() 為極點,以
為極點,以 ![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線 ![]() 的極坐標方程為
的極坐標方程為 ![]() .
.
(1)求曲線 ![]() 的普通方程與曲線
的普通方程與曲線 ![]() 的直角坐標方程;
的直角坐標方程;
(2)試判斷曲線 ![]() 與
與 ![]() 是否存在兩個交點,若存在,求出兩交點間的距離;若不存在,說明理由.
是否存在兩個交點,若存在,求出兩交點間的距離;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 和拋物線
和拋物線![]() 交于
交于![]() 兩點,且直線
兩點,且直線![]() 恰好通過橢圓
恰好通過橢圓![]() 的右焦點
的右焦點![]() ,
,
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)經過![]() 的直線
的直線![]() 和橢圓
和橢圓![]() 交于
交于![]() 兩點,交拋物線于
兩點,交拋物線于![]() 兩點,
兩點, ![]() 是拋物線的焦點,是否存在直線
是拋物線的焦點,是否存在直線![]() ,使得
,使得![]() ,若存在,求出直線
,若存在,求出直線![]() 的方程,若不存在,說明理由。
的方程,若不存在,說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,四個頂點構成的菱形的面積是4,圓
,四個頂點構成的菱形的面積是4,圓![]() 過橢圓
過橢圓![]() 的上頂點
的上頂點![]() 作圓
作圓![]() 的兩條切線分別與橢圓
的兩條切線分別與橢圓![]() 相交于
相交于![]() 兩點(不同于點
兩點(不同于點![]() ),直線
),直線![]() 的斜率分別為
的斜率分別為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)當![]() 變化時,①求
變化時,①求![]() 的值;②試問直線
的值;②試問直線![]() 是否過某個定點?若是,求出該定點;若不是,請說明理由.
是否過某個定點?若是,求出該定點;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,
, ![]() ,函數
,函數![]() ,函數
,函數![]() 在
在![]() 軸上的截距我
軸上的截距我![]() ,與
,與![]() 軸最近的最高點的坐標是
軸最近的最高點的坐標是![]() .
.
(Ⅰ)求函數![]() 的解析式;
的解析式;
(Ⅱ)將函數![]() 的圖象向左平移
的圖象向左平移![]() (
(![]() )個單位,再將圖象上各點的縱坐標不變,橫坐標伸長到原來的2倍,得到函數
)個單位,再將圖象上各點的縱坐標不變,橫坐標伸長到原來的2倍,得到函數![]() 的圖象,求
的圖象,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com