
【題目】設函數![]() (
(![]() ).
).
(1)試討論函數![]() 的單調性;
的單調性;
(2)設![]() ,記
,記![]() ,當
,當![]() 時,若函數
時,若函數![]() 與函數
與函數![]() 有兩個不同交點
有兩個不同交點![]() ,
,![]() ,設線段的中點為
,設線段的中點為![]() ,試問s是否為
,試問s是否為![]() 的根?說明理由.
的根?說明理由.
【答案】(1)見解析;(2)s不是![]() 的根,理由見解析
的根,理由見解析
【解析】
(1)求解函數的導函數,分類討論可得:①若![]() 時,當
時,當![]() 時,函數
時,函數![]() 單調遞減,當
單調遞減,當![]() 時,函數
時,函數![]() 單調遞增; ②若
單調遞增; ②若![]() 時,函數
時,函數![]() 單調遞增; ③若
單調遞增; ③若![]() 時,當
時,當![]() 時,函數
時,函數![]() 單調遞減,當
單調遞減,當![]() 時,函數
時,函數![]() 單調遞增.
單調遞增.
(2)構造新函數![]() ,
,![]() 求解導函數可得
求解導函數可得![]() ,欲證
,欲證![]() ,故只需證明.
,故只需證明.![]() , 由于
, 由于![]() ,
,![]() 是方程
是方程![]() 的兩個不相等的實根,不妨設為
的兩個不相等的實根,不妨設為![]() ,代入方程化簡可得
,代入方程化簡可得![]() ,故只需證明
,故只需證明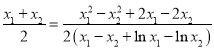 ,化簡為
,化簡為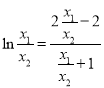 ,構造
,構造 ![]() ,
,![]() ,通過求導可知
,通過求導可知![]() 在
在![]() 單調遞增.又
單調遞增.又![]() ,因此
,因此![]() 即可證明
即可證明![]() 不成立.
不成立.
(1)由![]() ,可知
,可知![]() .
.
因為函數![]() 的定義域為
的定義域為![]() ,所以,
,所以,
①若![]() 時,當
時,當![]() 時,
時,![]() ,函數
,函數![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增;
單調遞增;
②若![]() 時,當
時,當![]() 在
在![]() 內恒成立,函數
內恒成立,函數![]() 單調遞增;
單調遞增;
③若![]() 時,當
時,當![]() 時,
時,![]() ,函數
,函數![]() 單調遞減,當
單調遞減,當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增.
單調遞增.
(2)證明:由題可知![]() (
(![]() ),
),
所以![]()
所以當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]()
欲證![]() ,故只需證明.
,故只需證明.![]()
設![]() ,
,![]() 是方程
是方程![]() 的兩個不相等的實根,不妨設為
的兩個不相等的實根,不妨設為![]() ,
,
則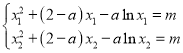
兩式相減并整理得![]() ,
,
從而![]() ,
,
故只需證明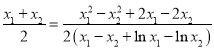 (*)
(*)
即![]() .所以(*)式可化為
.所以(*)式可化為![]() ,即
,即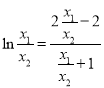
因為![]() ,所以
,所以![]() ,不妨令
,不妨令![]() ,即證
,即證![]() ,
,![]() 成立.
成立.
記![]() ,
,![]() ,所以
,所以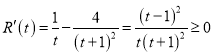 ,當且僅當
,當且僅當![]() 時,等號成立,
時,等號成立,
因此![]() 在
在![]() 單調遞增.又
單調遞增.又![]() ,因此
,因此![]() ,
,![]() ,故
,故![]() ,
,![]() ,即
,即![]() 不成立.
不成立.
故s不是![]() 的根得證.
的根得證.


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源: 題型:
【題目】新型冠狀病毒屬于![]() 屬的冠狀病毒,人群普遍易感,病毒感染者一般有發熱咳嗽等臨床表現,現階段也出現無癥狀感染者.基于目前的流行病學調查和研究結果,病毒潛伏期一般為1-14天,大多數為3-7天.為及時有效遏制病毒擴散和蔓延,減少新型冠狀病毒感染對公眾健康造成的危害,需要對與確診新冠肺炎病人接觸過的人員進行檢查.某地區對與確診患者有接觸史的1000名人員進行檢查,檢查結果統計如下:
屬的冠狀病毒,人群普遍易感,病毒感染者一般有發熱咳嗽等臨床表現,現階段也出現無癥狀感染者.基于目前的流行病學調查和研究結果,病毒潛伏期一般為1-14天,大多數為3-7天.為及時有效遏制病毒擴散和蔓延,減少新型冠狀病毒感染對公眾健康造成的危害,需要對與確診新冠肺炎病人接觸過的人員進行檢查.某地區對與確診患者有接觸史的1000名人員進行檢查,檢查結果統計如下:
發熱且咳嗽 | 發熱不咳嗽 | 咳嗽不發熱 | 不發熱也不咳嗽 | |
確診患病 | 200 | 150 | 80 | 30 |
確診未患病 | 150 | 150 | 120 | 120 |
(1)能否在犯錯率不超過0.001的情況下,認為新冠肺炎密切接觸者有發熱癥狀與最終確診患病有關.
臨界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.645 | 7.879 | 10.828 |
(2)在全國人民的共同努力下,尤其是全體醫護人員的辛勤付出下,我國的疫情得到較好控制,現階段防控重難點主要在境外輸入病例和無癥狀感染者(即無相關臨床表現但核酸檢測或血清特異性免疫球蛋白M抗體檢測陽者).根據防控要求,無癥狀感染者雖然還沒有最終確診患2019新冠肺炎,但與其密切接觸者仍然應當采取居家隔離醫學觀察14天,已知某人曾與無癥狀感染者密切接觸,而且在家已經居家隔離10天未有臨床癥狀,若該人員居家隔離第![]() 天出現臨床癥狀的概率為
天出現臨床癥狀的概率為![]() ,
,![]() ,兩天之間是否出現臨床癥狀互不影響,而且一旦出現臨床癥狀立刻送往醫院核酸檢查并采取必要治療,若14天內未出現臨床癥狀則可以解除居家隔離,求該人員在家隔離的天數(含有臨床癥狀表現的當天)
,兩天之間是否出現臨床癥狀互不影響,而且一旦出現臨床癥狀立刻送往醫院核酸檢查并采取必要治療,若14天內未出現臨床癥狀則可以解除居家隔離,求該人員在家隔離的天數(含有臨床癥狀表現的當天)![]() 的分布列以及數學期望值.(保留小數點后兩位)
的分布列以及數學期望值.(保留小數點后兩位)
查看答案和解析>>
科目:高中數學 來源: 題型:
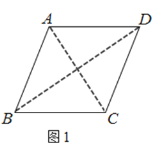
【題目】已知四邊形![]() 是邊長為5的菱形,對角線
是邊長為5的菱形,對角線![]() (如圖1),現以
(如圖1),現以![]() 為折痕將菱形折起,使點
為折痕將菱形折起,使點![]() 達到點
達到點![]() 的位置,棱
的位置,棱![]() ,
,![]() 的中點分為
的中點分為![]() ,
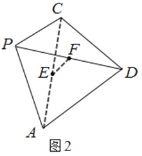
,![]() ,且四面體
,且四面體![]() 的外接球球心落在四面體內部(如圖2),則線段
的外接球球心落在四面體內部(如圖2),則線段![]() 長度的取值范圍為________.
長度的取值范圍為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義行列式的運算如下: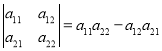 ,已函數
,已函數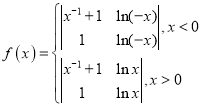 以下命題正確的是( )
以下命題正確的是( )
①對![]() ,都有
,都有![]() ;②若
;②若![]() ,對
,對![]() ,總存在非零常數了,使得
,總存在非零常數了,使得![]() ;③若存在直線
;③若存在直線![]() 與
與![]() 的圖象無公共點,且使
的圖象無公共點,且使![]() 的圖案位于直線兩側,此直線即稱為函數
的圖案位于直線兩側,此直線即稱為函數![]() 的分界線.則
的分界線.則![]() 的分界線的斜率的取值范圍是
的分界線的斜率的取值范圍是![]() ;④函數
;④函數![]() 的零點有無數個.
的零點有無數個.
A.①③④B.①②④
C.②③D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“今年我已經8個月沒有戲拍了”迪麗熱巴在8月的一檔綜藝節目上說,霍建華在家里開玩笑時說到“我失業很久了”;明道也在參加《演員請就位》時透露,已經大半年沒有演過戲.為了了解演員的生存現狀,什么樣的演員才有戲演,有人搜集了內地、港澳臺共計9481名演員的演藝生涯資料,在統計的所有演員資料后得到以下結論:①有![]() 的人在2019年沒有在影劇里露過臉;②2019年備案的電視劇數量較2016年時下滑超過三分之一;③女演員面臨的競爭更加激烈;④演員的艱難程度隨著年齡的增加而降低.請問:以下判斷正確的是( )
的人在2019年沒有在影劇里露過臉;②2019年備案的電視劇數量較2016年時下滑超過三分之一;③女演員面臨的競爭更加激烈;④演員的艱難程度隨著年齡的增加而降低.請問:以下判斷正確的是( )
A.調查采用了分層抽樣B.調查采用了簡單隨機抽樣
C.調查采用了系統抽樣D.非抽樣案例
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻折成
翻折成![]() .若
.若![]() 為線段
為線段![]() 的中點.
的中點.
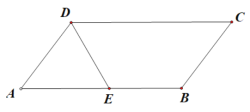
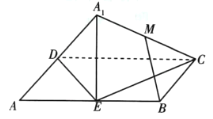
(1)證明![]() 平面
平面![]() ,并求
,并求![]() 的長;
的長;
(2)在翻折過程中,當三棱錐![]() 的體積取最大時,求平面
的體積取最大時,求平面![]() 與平面
與平面![]() 所成的二面角的余弦值.
所成的二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() (其中
(其中![]() ,點P的軌跡記為曲線
,點P的軌跡記為曲線![]() ,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,點Q在曲線
,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,點Q在曲線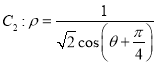 上.
上.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)當![]() ,
,![]() 時,求曲線
時,求曲線![]() 與曲線
與曲線![]() 的公共點的極坐標
的公共點的極坐標
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com