
【題目】如圖所示,在正方體ABCD﹣A1B1C1D1中,M,E,F,N分別為A1B1 , B1C1 , C1D1 , D1A1的中點,求證: 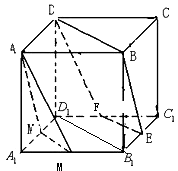
(1)E,F,D,B四點共面;
(2)面AMN∥平面EFDB.
【答案】
(1)證明:∵E,E分別是B1C1,C1D1的中點,
∴EF∥B1D1,
∵B1D1∥BD,∴EF∥BD,
∴E,F,B,D,四點共面.
(2)證明:∵M,N分別是A1B1,D1A1的中點,
∴MN∥B1D1,
∵EF∥B1D1,∴MN∥EF,
∵F,N分別是D1C1、A1B1的中點,
∴NF ![]() A1D1,
A1D1,
∵ ![]() ,∴NF
,∴NF ![]() AC,
AC,
∴四邊形NFCA是平行四邊形,
∴AN∥CF,
∵MN∩AN=N,EF∩DF=F,
∴面MAN∥面EFDB.
【解析】(1)由E,E分別是B1C1 , C1D的中點,知EF∥B1D1 , 從而得到EF∥BD,由此能證明E,F,B,D,四點共面.(2)由題設條件推導出MN∥EF,AN∥CF,由此能夠證明面MAN∥面EFDB.
【考點精析】本題主要考查了平面的基本性質及推論和直線與平面平行的性質的相關知識點,需要掌握如果一條直線上的兩點在一個平面內,那么這條直線在此平面內;過不在一條直線上的三點,有且只有一個平面;如果兩個不重合的平面有一個公共點,那么它們有且只有一條過該點的公共直線;一條直線與一個平面平行,則過這條直線的任一平面與此平面的交線與該直線平行;簡記為:線面平行則線線平行才能正確解答此題.


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程  (t為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為:ρ=4cosθ.
(t為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為:ρ=4cosθ.
(1)把直線l的參數方程化為極坐標方程,把曲線C的極坐標方程化為普通方程;
(2)求直線l與曲線C交點的極坐標(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)對任意實數x,y均有f(x)=f( ![]() )+f(
)+f( ![]() ).當x>0時,f(x)>0
).當x>0時,f(x)>0
(1)判斷函數f(x)在R上的單調性并證明;
(2)設函數g(x)與函數f(x)的奇偶性相同,當x≥0時,g(x)=|x﹣m|﹣m(m>0),若對任意x∈R,不等式g(x﹣1)≤g(x)恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點A,B是單位圓O上的兩點,A,B點分別在第一,而象限,點C是圓O與x軸正半軸的交點,若∠COA=60°,∠AOB=α,點B的坐標為(﹣ ![]() ,
, ![]() ).
). 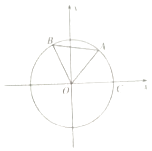
(1)求sinα的值;
(2)已知動點P沿圓弧從C點到A點勻速運動需要2秒鐘,求動點P從A點開始逆時針方向作圓周運動時,點P的縱坐標y關于時間t(秒)的函數關系式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線y2=2px(p>0),F為其焦點,l為其準線,過F作一條直線交拋物線于A,B兩點,A′,B′分別為A,B在l上的射線,M為A′B′的中點,給出下列命題: ①A′F⊥B′F;
②AM⊥BM;
③A′F∥BM;
④A′F與AM的交點在y軸上;
⑤AB′與A′B交于原點.
其中真命題的是 . (寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=ln ![]() ,則f(x)是( )
,則f(x)是( )
A.奇函數,且在(0,+∞)上單調遞減
B.奇函數,且在(0,+∞)上單凋遞增
C.偶函數,且在(0,+∞)上單調遞減
D.偶函數,且在(0,+∞)上單凋遞增
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,E為棱CC1上的動點. 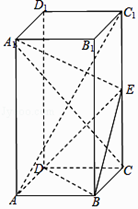
(1)若E為棱CC1的中點,求證:A1E⊥平面BDE;
(2)試確定E點的位置使直線A1C與平面BDE所成角的正弦值是 ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com