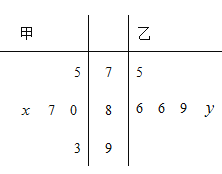
【題目】在學校組織的英語單詞背誦比賽中，5位評委對甲、乙兩名同學的評分如莖葉圖所示（分數為整數，且滿分100分），若甲同學所得評分的中位數為87，乙同學所得評分的唯一眾數為86，則甲同學所得評分的平均數不小于乙同學所得評分的平均數的概率為______．
科目：高中數學 來源： 題型：
【題目】求滿足下列條件的橢圓或雙曲線的標準方程：
（1）橢圓的焦點在
軸上，焦距為4，且經過點
；
（2）雙曲線的焦點在
軸上，右焦點為
，過作重直于軸的直線交雙曲線于
，
兩點，且
，離心率為
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2019年4月20日，重慶市實施高考改革方案，2018年秋季入學的高中一年級的學生將實行“
”模式.即“3”為全國統考科目語文、數學、外語所有學生必考；“1”為物理、歷史科目中選擇一科俗稱“2選1”；“2”為再選學科，考生可在化學、生物、思想政治、地理4個科目中選擇兩科俗稱“4選2”，選擇學科完全相同即為相同“組合”.某校高一年級有三名同學甲，乙，丙根據自己喜歡的大學和專業情況均選擇了物理，為了了解“4選2”選科情況老師找這三名同學來談話情況如下：
甲說：我選了化學，但沒有選思想政治；
乙說：我與甲有一科相同，但沒有選化學和地理；
丙說：我與甲有相同的選科，與乙也有相同選科，但我們三個選的“組合”都不相同.則下列結論正確的是（ ）
A.甲選了化學和地理B.丙可能選化學和思想政治
C.甲一定選地理D.丙一定選了生物和地理
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】交強險是車主必須為機動車購買的險種，若普通
座以下私家車投保交強險第一年的費用（基準保費）統一為
元，在下一年續保時，實行的是費率浮動機制，保費與上一年度車輛發生道路交通事故的情況相聯系，發生交通事故的次數越多，費率也就越高，具體浮動情況如下表：
交強險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
| 上一年度未發生有責任道路交通事故 | 下浮 |
| 上兩年度未發生有責任道路交通事故 | 下浮 |
| 上三年度未發生有責任道路交通事故 | 下浮 |
| 上一個年度發生一次有責任不涉及死亡的道路交通事故 |
|
| 上一個年度發生兩次及兩次以上有責任不涉及死亡的道路交通事故 | 上浮 |
| 上一個年度發生有責任交通死亡事故 | 上浮 |
某機構為了解某一品牌普通座以下私家車的投保情況，隨機抽取了
輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況，統計得到了下面的表格：
類型 |
|
|
|
|
|
數量 |
|
|
|
|
|
以這輛該品牌車的投保類型的頻率代替一輛車投保類型的概率，完成下列問題：
（1）按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規定，
，記
為某同學家的一輛該品牌車在第四年續保時的費用，求的分布列與數學期望；（數學期望值保留到個位數字）
（2）某二手車銷售商專門銷售這一品牌的二手車，且將下一年的交強險保費高于基本保費的車輛記為事故車，假設購進一輛事故車虧損
元，一輛非事故車盈利
元:
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車，求這三輛車中至多有一輛事故車的概率；
②若該銷售商一次購進
輛(車齡已滿三年)該品牌二手車，求他獲得利潤的期望值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的左右焦點分別為
、
，橢圓的離心率為
，
為橢圓上任意一點，
的最大面積為
．
（1）求橢圓
的標準方程；
（2）過的直線
與橢圓交于
、
兩點，連接
、
，若
的內切圓面積為
，則求直線方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
是圓
上的一動點，點
在直線
上線段
的垂直平分線交直線
于點
．
（1）若點的軌跡為橢圓，則求
的取值范圍；
（2）設
時對應的橢圓為
，
為橢圓的右頂點，直線
與交于
、
兩點，若
，求
面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列五個命題：
①凈
三種個體按
的比例分層抽樣調查，如果抽取的
個體為9個，則樣本容易為30；②一組數據1、2、3、4、5的平均數、眾數、中位數相同；③甲組數據的方差為5，乙組數據為5、6、9、10、5，那么這兩組數據中較穩定的是甲；④已知具有線性相關關系的兩個變量滿足的回歸直線方程為
．則
每增加1個單位，
平均減少2個單位；⑤統計的10個樣本數據為125，120，122，105，130，114，116，95，120，134，則樣本數據落在
內的頻率為0.4其中真命題為（ ）
A. ①②④B. ②④⑤C. ②③④D. ③④⑤
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-5：不等式選講]
已知函數f（x）=|2x﹣1|+|x+1|，g（x）=|x﹣a|+|x+a|．
（Ⅰ）解不等式f（x）＞9；
（Ⅱ）x1∈R，x2∈R，使得f（x1）=g（x2），求實數a的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
