
���}Ŀ��ij�ЌW�S�C��ȡ���ָ�һ�W���{(di��o)����ÿ���������ŌW���ĕr�g����λ����犣����������Ô�(sh��)��(j��)�L�Ƴ���D��ʾ���l�ʷֲ�ֱ���D�������������ŌW���r�g�ķ�����![]() ���ӱ���(sh��)��(j��)�ֽM��
���ӱ���(sh��)��(j��)�ֽM��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
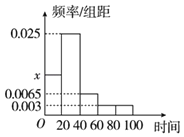
��������ֱ���D��![]() ��ֵ��
��ֵ��
�������ČWУȫ�w��һ�W�������x![]() ���W�����@
���W�����@![]() ���W�����������ŌW���r�g����
���W�����������ŌW���r�g����![]() ��犵��˔�(sh��)ӛ��
��犵��˔�(sh��)ӛ��![]() ����
����![]() �ķֲ��к͔�(sh��)�W����������ֱ���D�е��l��������ʣ���
�ķֲ��к͔�(sh��)�W����������ֱ���D�е��l��������ʣ���
���𰸡�������![]() ���������ֲ���Ҋ������
���������ֲ���Ҋ������![]() .
.
��������
����������ֱ���D�о�����e�ĺ͞�![]() ��ֱ�����
��ֱ�����![]() ���ɣ�
���ɣ�
���������}���![]() ���S�C׃��
���S�C׃��![]() �����п���ȡֵ��
�����п���ȡֵ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���ɴ������
���ɴ������![]() �ķֲ��м��䔵(sh��)�W������
�ķֲ��м��䔵(sh��)�W������
�����������l�ʷֲ�ֱ���D�����о�����e֮�͞�![]() ��
��
�ɵ�![]() �����
�����![]() ��
��
���������l�ʷֲ�ֱ���D��֪��ȫ�w��һ�W���У��������ŌW���r�g����![]() ��犵ČW�����l�ʞ�
��犵ČW�����l�ʞ�![]() ��
��
![]() �Ŀ���ȡֵ��
�Ŀ���ȡֵ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��
![]() ���S�C׃��
���S�C׃��![]() �ķֲ������±���ʾ��
�ķֲ������±���ʾ��
|
|
|
|
|
|
|
|
|
|
|
|
���ԣ��S�C׃��![]() �Ĕ�(sh��)�W������
�Ĕ�(sh��)�W������![]() ��
��


 ���n��ͬ��Ӗ��ϵ�д�
���n��ͬ��Ӗ��ϵ�д� һ���������㑪���}���쾚һ��ȫϵ�д�
һ���������㑪���}���쾚һ��ȫϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ�����ں���(sh��)![]() �����ڶ��x���(n��i)���ڌ���(sh��)
�����ڶ��x���(n��i)���ڌ���(sh��)![]() ���M��
���M��![]() ���t�Q
���t�Q![]() �顰�ֲ��溯��(sh��)��.
�顰�ֲ��溯��(sh��)��.
(1)��֪���κ���(sh��)![]() ��ԇ�Д�
��ԇ�Д�![]() �Ƿ�顰�ֲ��溯��(sh��)�������f�����ɣ�
�Ƿ�顰�ֲ��溯��(sh��)�������f�����ɣ�
(2)��![]() �Ƕ��x�څ^(q��)�g
�Ƕ��x�څ^(q��)�g![]() �ϵġ��ֲ��溯��(sh��)������(sh��)
�ϵġ��ֲ��溯��(sh��)������(sh��)![]() ��ȡֵ������
��ȡֵ������
(3)��![]() �鶨�x��
�鶨�x��![]() �ϵġ��ֲ��溯��(sh��)������(sh��)
�ϵġ��ֲ��溯��(sh��)������(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ���д�ˮ�¿��Ż���У���ˮ�T�蝓��ˮ���30��ˮ���M�����I(y��)�������������������������棺�����r��ƽ���ٶȞ�ÿ���![]() �ף�ÿ��犵���������
�ף�ÿ��犵���������![]() ������ˮ�����I(y��)��Ҫ10��犣�ÿ��犵���������0.3�����۷���ˮ��r���ٶȞ�ÿ���
������ˮ�����I(y��)��Ҫ10��犣�ÿ��犵���������0.3�����۷���ˮ��r���ٶȞ�ÿ���![]() �ף�ÿ�����������0.2�����O��ˮ�T�ڴ˴ο��Ż���еĿ���������
�ף�ÿ�����������0.2�����O��ˮ�T�ڴ˴ο��Ż���еĿ���������![]() ����
����
��1����![]() ��ʾ��
��ʾ��![]() �ĺ���(sh��)��
���(sh��)��
��2����![]() ����������
����������![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����D���������F![]() �У�
�У�![]() ƽ��
ƽ��![]() ������
������![]() ��ֱ�����Σ�����
��ֱ�����Σ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �ϵ��c����
�ϵ��c����![]() ��
��
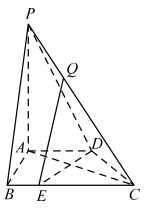
��1�����C��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ��
������ֵ��
��3���O![]() ����
����![]() �ϵ��c�����c
�ϵ��c�����c![]() ��
��![]() �غϣ�����ֱ��
�غϣ�����ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ���O��(sh��)��![]() �M��
�M��![]() ������A��B�ǃɂ��_���Č���(sh��)��
������A��B�ǃɂ��_���Č���(sh��)��![]()
��1����![]() ����
����![]() ��ǰn헺ͣ�
��ǰn헺ͣ�
��2���C����![]() ���ǵȱȔ�(sh��)�У�
���ǵȱȔ�(sh��)�У�
��3����![]() ����(sh��)��
����(sh��)��![]() �г�ȥ�_ʼ�ă���⣬�Ƿ�߀����ȵă�헣����C����ĽYՓ.
�г�ȥ�_ʼ�ă���⣬�Ƿ�߀����ȵă�헣����C����ĽYՓ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����һ���L��![]() ������
������![]() �ľ����FƤ����D1��������һ��ֱ�LjA�Ώ��ܣ���D3�������ھ��ε����g��һ�l�����������������_�������õăɲ��ַքe�����w�e��ȵ�б�؈A�����D2����Ȼ������һ���m�����D(zhu��n)ƴ�ӳ�ֱ�LjA�Ώ��ܣ���D3������Ӌƴ�ӓp�IJ��֣�����ʹ��ֱ�LjA�Ώ��ܵ��w�e���
�ľ����FƤ����D1��������һ��ֱ�LjA�Ώ��ܣ���D3�������ھ��ε����g��һ�l�����������������_�������õăɲ��ַքe�����w�e��ȵ�б�؈A�����D2����Ȼ������һ���m�����D(zhu��n)ƴ�ӳ�ֱ�LjA�Ώ��ܣ���D3������Ӌƴ�ӓp�IJ��֣�����ʹ��ֱ�LjA�Ώ��ܵ��w�e���
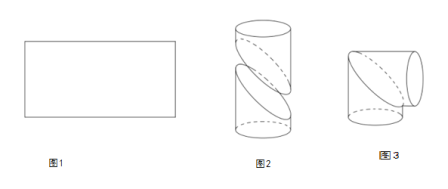
��1����ֱ�LjA�Ώ��ܣ��D3�����w�e��
��2����б����E�A�Ľ��ࣻ
��3���������ĈD1�н����m��?sh��)�����ϵ��ʹ�����������ķ��̞�![]() ��������̲��������D��
��������̲��������D��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����D,��ƽ����߅��ABCD��,![]() ,��߅��ACEF��������,��ƽ��
,��߅��ACEF��������,��ƽ��![]() ƽ��ACEF.
ƽ��ACEF.
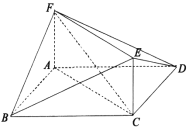
(1)�C��:![]() ;
;
(2)��ƽ��BEF�cƽ��BCF�����J����ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]()
![]() �L�S�L����S�L�ăɱ����B�Y�E�A���Ă���c�õ������ε���e��4��ֱ��
�L�S�L����S�L�ăɱ����B�Y�E�A���Ă���c�õ������ε���e��4��ֱ��![]() �^�c
�^�c![]() �����c�E�A�ཻ����һ�c
�����c�E�A�ཻ����һ�c![]() .
.
��1����E�A�ķ��̣�
��2��������![]() �L��
�L��![]() ����ֱ��
����ֱ��![]() �ăAб�ǣ�
�ăAб�ǣ�
��3���c![]() �ھ���
�ھ���![]() �Ĵ�ֱƽ�־��ϣ���
�Ĵ�ֱƽ�־��ϣ���![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ�� �}�ͣ�
���}Ŀ������(sh��)a��b�M��ab��0��a��b����a��b��![]() ��
��![]() ��һ����ɵĔ�(sh��)�У�������
��һ����ɵĔ�(sh��)�У�������
A. �����ǵȲ(sh��)�У�Ҳ�����ǵȱȔ�(sh��)��
B. �����ǵȲ(sh��)�У����������ǵȱȔ�(sh��)��
C. �������ǵȲ(sh��)�У��������ǵȱȔ�(sh��)��
D. �������ǵȲ(sh��)�У�Ҳ�������ǵȱȔ�(sh��)��
�鿴�𰸺ͽ���>>
���H�WУ��(y��u)�x - �������б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙��e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com