
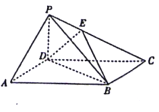
【題目】如圖所示,在四棱錐![]() 中,底要
中,底要![]() 為平行四邊形,
為平行四邊形, ![]() ,
,
![]() ,
, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() 為
為![]() 上一點,且
上一點,且![]() .
.
(1)證明: ![]() ;
;
(2)求二面角![]() 余弦值.
余弦值.
【答案】(1)詳見解析(2)![]()
【解析】試題分析:(1)由![]() 底面
底面![]() ,得
,得![]() ,再利用余弦定理計算AD,根據(jù)勾股定理得
,再利用余弦定理計算AD,根據(jù)勾股定理得![]() ,利用線面垂直判定定理可得
,利用線面垂直判定定理可得![]() ,最后根據(jù)線面垂直性質(zhì)定理得
,最后根據(jù)線面垂直性質(zhì)定理得![]() ;(2)利用空間向量數(shù)量積求二面角的余弦值,先根據(jù)條件建立恰當(dāng)空間直角坐標(biāo)系,設(shè)立各點坐標(biāo),利用方程組解出各面法向量,利用向量數(shù)量積求法向量夾角,最后根據(jù)二面角與法向量夾角關(guān)系確定所求值.
;(2)利用空間向量數(shù)量積求二面角的余弦值,先根據(jù)條件建立恰當(dāng)空間直角坐標(biāo)系,設(shè)立各點坐標(biāo),利用方程組解出各面法向量,利用向量數(shù)量積求法向量夾角,最后根據(jù)二面角與法向量夾角關(guān)系確定所求值.
試題解析:(1)證明:在![]() 中,
中, ![]() .
.
不妨設(shè)![]() ,則由已知
,則由已知![]() ,得
,得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,又
,又![]() 底面
底面![]() ,所以
,所以![]()
所以 .
.
(2)解:由(1)知![]() ,
, ![]() ,以
,以![]() 為原點,如圖所示建立空間直角坐標(biāo)系
為原點,如圖所示建立空間直角坐標(biāo)系![]() ,設(shè)
,設(shè)![]() ,
,
于是![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
因為![]() 為
為![]() 上一點,且
上一點,且![]() ,所以
,所以![]() ,所以
,所以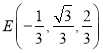 ,
,
所以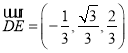 ,
,![]() ,設(shè)平面
,設(shè)平面![]() 的法向量
的法向量![]() ,
,
則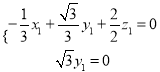 ,令
,令![]() ,則
,則![]()
又![]() ,
, ,設(shè)平面
,設(shè)平面![]() 的法向量
的法向量![]()
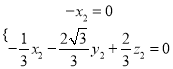 ,令
,令![]() ,則
,則![]() ,
,
設(shè)二面角![]() 的大小為
的大小為![]() ,由圖可知
,由圖可知![]() ,則
,則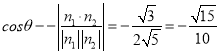 .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】(文科)已知的橢圓![]() 的左、右兩個焦點分別為
的左、右兩個焦點分別為![]() ,上頂點
,上頂點![]() ,
, ![]() 是正三角形且周長為6.
是正三角形且周長為6.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程及離心率;
的標(biāo)準(zhǔn)方程及離心率;
(2) ![]() 為坐標(biāo)原點,
為坐標(biāo)原點, ![]() 是直線
是直線![]() 上的一個動點,求
上的一個動點,求![]() 的最小值,并求出此時點
的最小值,并求出此時點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
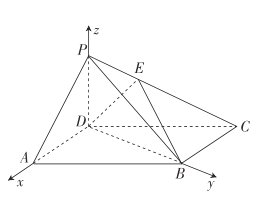
【題目】如圖,在三棱錐P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D為線段AC的中點,E為線段PC上一點.

(1)求證:PA⊥BD;
(2)求證:平面BDE⊥平面PAC;
(3)當(dāng)PA∥平面BDE時,求三棱錐E-BCD的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() ,動點
,動點![]() ,
, ![]() 分別在
分別在![]() 軸,
軸, ![]() 軸上運動,
軸上運動, ![]() ,
, ![]() 為平面上一點,
為平面上一點, ![]() ,過點
,過點![]() 作
作![]() 平行于
平行于![]() 軸交
軸交![]() 的延長線于點
的延長線于點![]() .
.
(Ⅰ)求點![]() 的軌跡曲線
的軌跡曲線![]() 的方程;
的方程;
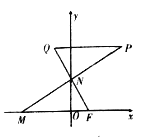
(Ⅱ)過![]() 點作
點作![]() 軸的垂線
軸的垂線![]() ,平行于
,平行于![]() 軸的兩條直線
軸的兩條直線![]() ,
, ![]() 分別交曲線
分別交曲線![]() 于
于![]() ,
, ![]() 兩點(直線
兩點(直線![]() 不過
不過![]() ),交
),交![]() 于
于![]() ,
, ![]() 兩點.若線段
兩點.若線段![]() 中點的軌跡方程為
中點的軌跡方程為![]() ,求
,求![]() 與
與![]() 的面積之比.
的面積之比.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】交強(qiáng)險是車主必須為機(jī)動車購買的險種,若普通6座以下私家車投保交強(qiáng)險第一年的費用(基準(zhǔn)保費)統(tǒng)一為![]() 元,在下一年續(xù)保時,實行的是費率浮動機(jī)制,保費與上一年度車輛發(fā)生道路交通事故的情況相聯(lián)系,發(fā)生交通事故的次數(shù)越多,費率也就是越高,具體浮動情況如下表:
元,在下一年續(xù)保時,實行的是費率浮動機(jī)制,保費與上一年度車輛發(fā)生道路交通事故的情況相聯(lián)系,發(fā)生交通事故的次數(shù)越多,費率也就是越高,具體浮動情況如下表:
交強(qiáng)險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
| 上一個年度未發(fā)生有責(zé)任道路交通事故 | 下浮10% |
| 上兩個年度未發(fā)生有責(zé)任道路交通事故 | 下浮20% |
| 上三個及以上年度未發(fā)生有責(zé)任道路交通事故 | 下浮30% |
| 上一個年度發(fā)生一次有責(zé)任不涉及死亡的道路交通事故 | 0% |
| 上一個年度發(fā)生兩次及兩次以上有責(zé)任道路交通事故 | 上浮10% |
| 上一個年度發(fā)生有責(zé)任道路交通死亡事故 | 上浮30% |
某機(jī)構(gòu)為了 某一品牌普通6座以下私家車的投保情況,隨機(jī)抽取了60輛車齡已滿三年的該品牌同型號私家車的下一年續(xù)保時的情況,統(tǒng)計得到了下面的表格:
類型 |
|
|
|
|
|
|
數(shù)量 | 10 | 5 | 5 | 20 | 15 | 5 |
以這60輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(1)按照我國《機(jī)動車交通事故責(zé)任強(qiáng)制保險條例》汽車交強(qiáng)險價格的規(guī)定, ![]() ,記
,記![]() 為某同學(xué)家的一輛該品牌車在第四年續(xù)保時的費用,求
為某同學(xué)家的一輛該品牌車在第四年續(xù)保時的費用,求![]() 的分布列與數(shù)學(xué)期望;(數(shù)學(xué)期望值保留到個位數(shù)字)
的分布列與數(shù)學(xué)期望;(數(shù)學(xué)期望值保留到個位數(shù)字)
(2)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強(qiáng)險保費高于基本保費的車輛記為事故車,假設(shè)購進(jìn)一輛事故車虧損5000元,一輛非事故車盈利10000元:
①若該銷售商購進(jìn)三輛(車齡已滿三年)該品牌二手車,求這三輛車中至多有一輛事故車的概率;
②若該銷售商一次購進(jìn)100輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列{an}的前n項和為Sn , S7=0,a3﹣2a2=12.
(1)求數(shù)列{an}的通項公式;
(2)求Sn﹣15n+50的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足a1=﹣ ![]() ,an+1=
,an+1= ![]() (n∈N+)
(n∈N+)
(1)證明數(shù)列{ ![]() }是等差數(shù)列并求{an}的通項公式.
}是等差數(shù)列并求{an}的通項公式.
(2)數(shù)列{bn}滿足bn= ![]() (n∈N+).求{bn}的前n項和Sn .
(n∈N+).求{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“大眾創(chuàng)業(yè),萬眾創(chuàng)新”是李克強(qiáng)總理在本屆政府工作報告中向全國人民發(fā)出的口號.某生產(chǎn)企業(yè)積極響應(yīng)號召,大力研發(fā)新產(chǎn)品.為了對新研發(fā)的一批產(chǎn)品進(jìn)行合理定價,將該產(chǎn)品按事先擬定的價格進(jìn)行試銷,得到一組銷售數(shù)據(jù)![]() ,如下表所示:
,如下表所示:

已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知變量![]() ,
, ![]() 具有線性相關(guān)關(guān)系,求產(chǎn)品銷量
具有線性相關(guān)關(guān)系,求產(chǎn)品銷量![]() (件)關(guān)于試銷單價
(件)關(guān)于試銷單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;
;
(3)用![]() 表示用正確的線性回歸方程得到的與
表示用正確的線性回歸方程得到的與![]() 對應(yīng)的產(chǎn)品銷量的估計值.當(dāng)銷售數(shù)據(jù)
對應(yīng)的產(chǎn)品銷量的估計值.當(dāng)銷售數(shù)據(jù)![]() 的殘差的絕對值
的殘差的絕對值![]() 時,則將銷售數(shù)據(jù)
時,則將銷售數(shù)據(jù)![]() 稱為一個“好數(shù)據(jù)”.現(xiàn)從6個銷售數(shù)據(jù)中任取2個,求抽取的2個銷售數(shù)據(jù)中至少有1個是“好數(shù)據(jù)”的概率.
稱為一個“好數(shù)據(jù)”.現(xiàn)從6個銷售數(shù)據(jù)中任取2個,求抽取的2個銷售數(shù)據(jù)中至少有1個是“好數(shù)據(jù)”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC三個頂點坐標(biāo)分別為:A(1,0),B(1,4),C(3,2),直線l經(jīng)過點(0,4).
(1)求△ABC外接圓⊙M的方程;
(2)若直線l與⊙M相交于P,Q兩點,且|PQ|=2 ![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com