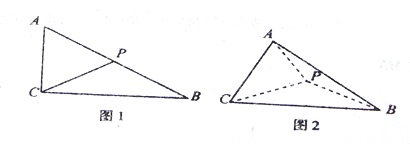
【題目】如圖1，在
中， 
， 
， 
， 
為
邊的中點，現把
沿
折疊，使其與
構成如圖2所示的三棱錐
，且
.
（1）求證：平面
平面
；
（2）求平面
與平面
夾角的余弦值.
【答案】(1)見解析(2) 
【解析】試題分析：（1）在圖1中，取CP的中點O，連接AO交CB于E，得AO⊥CP，在△OCB中，有AO⊥OB，即AO⊥平面PCB，
可證平面ACP⊥平面CPB．
（2）因為AO⊥平面CPB，且OC⊥OE，故可如圖建立空間直角坐標系，則
， 
，求出平面的法向量，利用向量夾角公式即可求解．
試題解析：
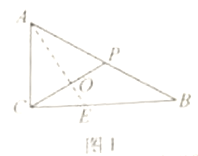
（1）如圖1，取
得中點
，連接
并延長交
于點
，
在
中，因為
， 
， 
， 
為
邊的中點，
所以
是正三角形，所以
，且
, 
, 
.
由折疊過程可知，在圖2中， 
， 
，如圖2，連接
，
在
中，由余弦定理得
，
所以
，所以
.又因為
， 
，
所以
，又因為
，所以平面
平面
.
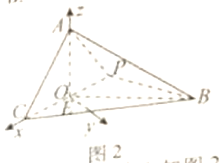
（2）因為
平面
，且
，所以可建立如圖二所示的空間直角坐標系.則
， 
， 
， 
， 
， 
， 
.
設平面
的一個法向量為
，則
由
得
.
同理可求得平面
的一個法向量為
.
設所求角為
，則所求角的余弦值
.
科目：高中數學 來源： 題型：
【題目】現從某學校高一年級男生中隨機抽取50名測量身高，測量發現被測學生身高全部介于
和
之間，將測量結果按如下方式分成6組：第1組
，第2組
，…，第6組
，下圖是按上述分組方法得到的頻率分布直方圖.
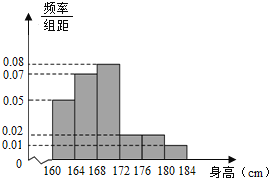
（1）求這50名男生身高的中位數，并估計該校高一全體男生的平均身高；
（2）求這50名男生當中身高不低于176
的人數，并且在這50名身高不低于176
的男生中任意抽取2人，求這2人身高都低于180
的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為比較甲、乙兩地某月12時的氣溫狀況，隨機選取該月中的5天，將這5天中12時的氣溫數據（單位：
）制成如圖所示的莖葉圖.考慮以下結論：
①甲地的平均氣溫低于乙地的平均氣溫；
②甲地的平均氣溫高于乙地的平均氣溫；
③甲地氣溫的標準差小于乙地氣溫的標準差；
④甲地氣溫的標準差大于乙地氣溫的標準差.
其中根據莖葉圖能得到的統計結論的標號為( )
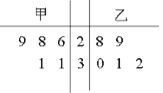
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
過點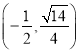
，且離心率為
.過點
的直線
與橢圓
交于
， 
兩點.
（Ⅰ）求橢圓
的標準方程；
（Ⅱ）若點
為橢圓
的右頂點，探究： 
是否為定值，若是，求出該定值，若不是，請說明理由.（其中， 
， 
分別是直線
、
的斜率）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在高中學習過程中，同學們常這樣說：“如果你的物理成績好，那么你的數學學習就不會有什么大問題．”某班針對“高中物理學習對數學學習的影響”進行研究，得到了學生的物理成績與數學成績具有線性相關關系，如表為該班隨機抽取6名學生在一次考試中的物理和數學成績：
學生編號 學科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成績（x） | 75 | 65 | 75 | 65 | 60 | 80 |
數學成績（y） | 125 | 117 | 110 | 103 | 95 | 110 |
（1）求數學成績y對物理成績x的線性回歸方程；
（2）該班某同學的物理成績100分，預測他的數學成績．
參考公式：回歸方程
中斜率和截距的最小二乘估計公式分別為：
，
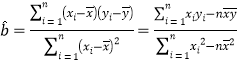參考數據：752+652+752+652+602+802＝29700，
75×125+65×117+75×110+65×103+60×95+80×110＝46425．
查看答案和解析>>
科目：高中數學 來源： 題型：
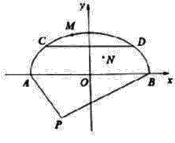
【題目】某經濟開發區規劃要修建一地下停車場，停車場橫截面是如圖所示半橢圓形AMB，其中AP為2百米，BP為4百米，
，M為半橢圓上異于A，B的一動點，且
面積最大值為
平方百米，如圖建系．
求出半橢圓弧的方程；
若要將修建地下停車場挖出的土運到指定位置P處，N為運土點，以A,B為出口，要使運土最省工，工程部需要指定一條分界線，請求出分界線所在的曲線方程；
若在半橢圓形停車場的上方修建矩形商場，矩形的一邊CD與AB平行，設
百米，試確定t的值，使商場地面的面積最大．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業為了了解職工的工作狀況，隨機抽取了一個車間對職工工作時間的情況進行暗訪，工作時間在
小時及以上的為合格.把所得數據進行整理后，分成
組畫出頻率分布直方圖（如圖所示），但由于工作疏忽，沒有畫出最后一組，只知道最后一組的頻數是
.
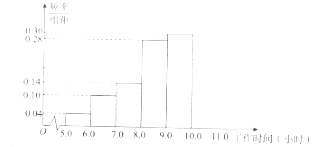
（Ⅰ）求這次暗訪中工作時間不合格的人數；
（Ⅱ）已知在工作時間超過
小時的人中有兩名女職工，現要從工作時間在
小時以上的人中選出兩名代表在職工代表大會上發言，求至少選出一位女職工作代表的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
