
【題目】2016年6月22 日,“國際教育信息化大會”在山東青島開幕.為了解哪些人更關注“國際教育信息化大會”,某機構隨機抽取了年齡在15-75歲之間的100人進行調查,經統計“青少年”與“中老年”的人數之比為9: 11.
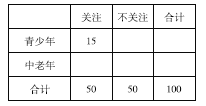
(1)根據已知條件完成下面的![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為“中老年”比“青少年”更加關注“國際教育信息化大會”;
的把握認為“中老年”比“青少年”更加關注“國際教育信息化大會”;
(2)現從抽取的青少年中采用分層抽樣的辦法選取9人進行問卷調查.在這9人中再選取3人進行面對面詢問,記選取的3人中關注“國際教育信息化大會”的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
附:參考公式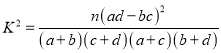 ,其中
,其中![]() .
.
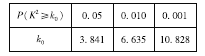
臨界值表:
【答案】(1)列聯表見解析,有![]() 的把握認為“中老年”比“青少年”更加關注“國際教育信息化大會”.
的把握認為“中老年”比“青少年”更加關注“國際教育信息化大會”.
(2)分布列見解析, ![]()
【解析】試題分析:(Ⅰ)根據統計數據,可得2×2列聯表,根據列聯表中的數據,計算K2的值,即可得到結論;
(Ⅱ)ξ的可能取值有0,1,2,3,求出相應的概率,可得ξ的分布列及數學期望.
試題解析:
解:(1)依題意可知,抽取的“青少年”共有![]() 人,“中老年”共有
人,“中老年”共有![]() 人.
人.
完成的![]() 列聯表如下:
列聯表如下:
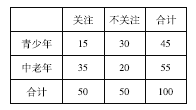
則
![]() ,
,
因為![]() ,所以有
,所以有![]() 的把握認為“中老年”比“青少年”更加關注“國際教育信息化大會”.
的把握認為“中老年”比“青少年”更加關注“國際教育信息化大會”.
(2)根據題意知選出關注的人數為3,不關注的人數為6,在這9人中再選取3人進行面對面詢問, ![]() 的取值可以為0,1,2,3,則
的取值可以為0,1,2,3,則
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
所以![]() 的分布列為
的分布列為
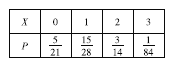
數學期望![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在正方體AC1中,過點A作平面A1BD的垂線,垂足為點H,則以下命題中,錯誤的命題是( ) 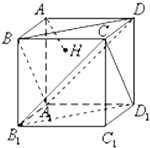
A.點H是△A1BD的垂心
B.AH的延長線經過點C1
C.AH垂直平面CB1D1
D.直線AH和BB1所成角為45°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an} 的前n項和Sn=3n2+8n,{bn}是等差數列,且an=bn+bn+1
(1)求數列{bn}的通項公式;
(2)令cn= ![]() ,求數列{cn}的前n項和Tn .
,求數列{cn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的奇函數,當x≥0時f(x)=2x﹣x2 ,
(1)求f(x)的表達式;
(2)設0<a<b,當x∈[a,b]時,f(x)的值域為 ![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com