
【題目】函數![]() (
(![]() ,
,![]() )的部分圖象如圖所示,則下列結論正確的是( )
)的部分圖象如圖所示,則下列結論正確的是( )
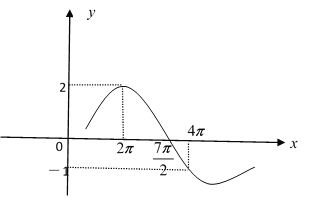
A.![]()
B.若把函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位,則所得函數是奇函數
個單位,則所得函數是奇函數
C.若把![]() 的橫坐標縮短為原來的
的橫坐標縮短為原來的![]() 倍,縱坐標不變,得到的函數在
倍,縱坐標不變,得到的函數在![]() 上是增函數
上是增函數
D.![]() ,若
,若![]() 恒成立,則
恒成立,則![]() 的最小值為
的最小值為![]()
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個頂點為
的一個頂點為![]() ,右焦點為
,右焦點為![]() ,且
,且![]() ,其中
,其中![]() 為原點.
為原點.
(Ⅰ)求橢圓的方程;
(Ⅱ)已知點![]() 滿足
滿足![]() ,點
,點![]() 在橢圓上(
在橢圓上(![]() 異于橢圓的頂點),直線
異于橢圓的頂點),直線![]() 與以
與以![]() 為圓心的圓相切于點
為圓心的圓相切于點![]() ,且
,且![]() 為線段
為線段![]() 的中點.求直線
的中點.求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網絡購物已經成為人們的一種生活方式.某購物平臺為了給顧客提供更好的購物體驗,為入駐商家設置了積分制度,每筆購物完成后,買家可以根據物流情況、商品質量等因素對商家做出評價,評價分為好評、中評和差評平臺規定商家有50天的試營業時間,期間只評價不積分,正式營業后,每個好評給商家計1分,中評計0分,差評計![]() 分,某商家在試營業期間隨機抽取100單交易調查了其商品的物流情況以及買家的評價情況,分別制成了圖1和圖2.
分,某商家在試營業期間隨機抽取100單交易調查了其商品的物流情況以及買家的評價情況,分別制成了圖1和圖2.
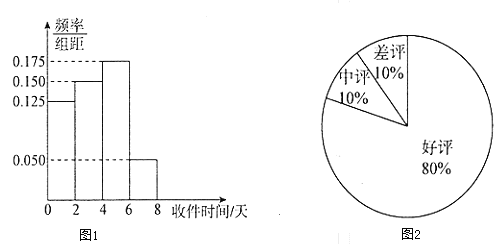
(1)通常收件時間不超過四天認為是物流迅速,否則認為是物流遲緩;
請根據題目所給信息完成下面![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為“獲得好評”與物流速度有關?
的把握認為“獲得好評”與物流速度有關?
好評 | 中評或差評 | 合計 | |
物流迅速 | |||
物流遲緩 | 30 | ||
合計 |
(2)從正式營業開始,記商家在每筆交易中得到的評價得分為![]() .該商家將試營業50天期間的成交情況制成了頻數分布表(表1),以試營業期間成交單數的頻率代替正式營業時成交單數發生的概率.
.該商家將試營業50天期間的成交情況制成了頻數分布表(表1),以試營業期間成交單數的頻率代替正式營業時成交單數發生的概率.
表1
成交單數 | 36 | 30 | 27 |
天數 | 10 | 20 | 20 |
(Ⅰ)求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)平臺規定,當積分超過10000分時,商家會獲得“誠信商家”稱號,請估計該商家從正式營業開始,1年內(365天)能否獲得“誠信商家”稱號
附: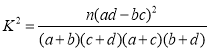
參考數據:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.
是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.
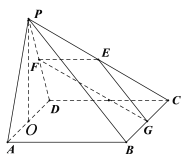
(Ⅰ)求證:PO平面![]() ;
;
(Ⅱ)求平面EFG與平面![]() 所成銳二面角的大小;
所成銳二面角的大小;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,若存在,求線段
,若存在,求線段![]() 的長度;若不存在,說明理由.
的長度;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】垃圾分類是對垃圾進行有效處置的一種科學管理方法.太原市為推進這項工作的實施,開展了“垃圾分類進小區”的評比活動.現有甲、乙兩個小區采取不同的宣傳與倡導方式對各自小區居民進行了有關垃圾分類知識的培訓,并參加了評比活動,評委會隨機從兩個小區各選出20戶家庭進行評比打分,每戶成績滿分為100分,評分后得到如下莖葉圖.
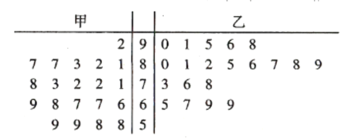
(1)依莖葉圖判斷哪個小區的平均分高?
(2)現從甲小區不低于80分的家庭中隨機抽取兩戶,求分數為87的家庭至少有一戶被抽中的概率;
(3)如果規定分數不低于85分的家庭為優秀,請填寫下面的![]() 列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為得分是否優秀與小區宣傳培訓方式有關?”
列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為得分是否優秀與小區宣傳培訓方式有關?”
甲 | 乙 | 合計 | |
優秀 |
|
| |
不優秀 |
|
| |
合計 |
參考公式和數據: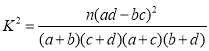 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間用一臺包裝機包裝葡萄糖,每袋葡萄糖的重量是一個隨機變量,它服從正態分布.當機器工作正常時,每袋葡萄糖平均重量![]() 為0.5kg,標準差
為0.5kg,標準差![]() 為0.015kg.
為0.015kg.
(1)已知包裝每袋葡萄糖的成本為1元,若發現包裝好的葡萄糖重量異常,則需要將該袋葡萄糖進行重新包裝,假設重新包裝后的葡萄糖重量正常.若某袋葡萄糖的重量![]() 滿足
滿足![]() ,則認為該袋葡萄糖重量正常. 問:在機器工作正常的情況下,至少包裝多少袋葡萄糖才能使“至少有一袋包裝好的葡萄糖重量正常”的概率大于0.98?并求出相應成本的最小期望值.
,則認為該袋葡萄糖重量正常. 問:在機器工作正常的情況下,至少包裝多少袋葡萄糖才能使“至少有一袋包裝好的葡萄糖重量正常”的概率大于0.98?并求出相應成本的最小期望值.
(2)某日開工后, 為檢査該包裝機工作是否正常, 隨機地抽取它所包裝的葡萄糖9袋,若抽取的9袋葡萄糖稱得凈重(kg)為:0.496, 0.508, 0.524, 0.519, 0.495, 0.510, 0.522, 0.513, 0.512.用樣本平均數![]() 作為
作為![]() 的估計值
的估計值![]() ,以
,以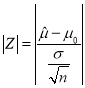 作為檢驗統計量,其中
作為檢驗統計量,其中![]() 為樣本總數,
為樣本總數,![]() 服從正態分布
服從正態分布![]() ,且
,且![]() .
.
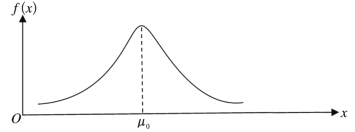
①若機器工作正常時, 每袋葡萄糖的重量服從的正態分布曲線如下圖所示,且經計算得上述樣本數據的標準差![]() 0.022.請在下圖(機器正常工作時的正態分布曲線)中,繪制出以該樣本作為估計得到的每袋葡萄糖所服從的正態分布曲線的草圖.
0.022.請在下圖(機器正常工作時的正態分布曲線)中,繪制出以該樣本作為估計得到的每袋葡萄糖所服從的正態分布曲線的草圖.
②若![]() ,就推斷該包裝機工作異常,這種推斷犯錯誤的概率不超過
,就推斷該包裝機工作異常,這種推斷犯錯誤的概率不超過![]() ,試以95%的可靠性估計該包裝機工作是否正常.
,試以95%的可靠性估計該包裝機工作是否正常.
附: 若隨機變量![]() 服從正態分布:
服從正態分布:![]() ,
,![]()
![]()
參考數據:![]() ;
;![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,其左、右焦點分別為
,其左、右焦點分別為![]() ,
,![]() ,點
,點![]() 為坐標平面內的一點,且
為坐標平面內的一點,且![]() ,
,![]() ,
,![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 為橢圓
為橢圓![]() 的左頂點,
的左頂點,![]() ,
,![]() 是橢圓
是橢圓![]() 上兩個不同的點,直線
上兩個不同的點,直線![]() ,
,![]() 的傾斜角分別為
的傾斜角分別為![]() ,
,![]() ,且
,且![]() .證明:直線
.證明:直線![]() 恒過定點,并求出該定點的坐標,
恒過定點,并求出該定點的坐標,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,由直三棱柱![]() 和四棱錐
和四棱錐![]() 構成的幾何體中,
構成的幾何體中,![]() ,平面
,平面![]() 平面
平面![]() .
.
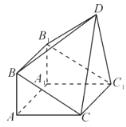
(1)求證:![]() ;
;
(2)在線段![]() 上(含端點)是否存在點P,使直線
上(含端點)是否存在點P,使直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ?若存在,求
?若存在,求![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com