
��֪����(sh��)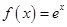 .
.
��1���O(sh��)����(sh��)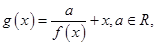 ��
��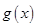 �ĘOֵ.
�ĘOֵ.
��2���C����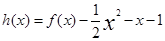 ��
�� �Ϟ�������(sh��)��
�Ϟ�������(sh��)��
��1�� ��(d��ng) �r(sh��)��
�r(sh��)�� �o(w��)�Oֵ����(d��ng)
�o(w��)�Oֵ����(d��ng) �r(sh��)��
�r(sh��)�� ��
�� ̎ȡ�ØOСֵ
̎ȡ�ØOСֵ ���o(w��)�O��ֵ�� ��2��Ҋ(ji��n)����
���o(w��)�O��ֵ�� ��2��Ҋ(ji��n)����
����ԇ�}��������1��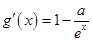 ,����Oֵ�r(sh��)Ҫ��(du��)����(sh��)
,����Oֵ�r(sh��)Ҫ��(du��)����(sh��) ӑՓ,�@Ȼ��(d��ng)
ӑՓ,�@Ȼ��(d��ng) �r(sh��)
�r(sh��) ��������(sh��),�o(w��)�Oֵ,��(d��ng)
��������(sh��),�o(w��)�Oֵ,��(d��ng) �r(sh��)�����
�r(sh��)����� �ĸ�,��ӑՓ�ɂ�(c��)�Ć��{(di��o)��;��2��Ҫ�C��������(sh��),���C��
�ĸ�,��ӑՓ�ɂ�(c��)�Ć��{(di��o)��;��2��Ҫ�C��������(sh��),���C�� ����,���ٴΌ�(du��)����(sh��)
����,���ٴΌ�(du��)����(sh��) �M(j��n)����(d��o)�о�����{(di��o)���c��ֵ,ֻҪ�f(shu��)��
�M(j��n)����(d��o)�о�����{(di��o)���c��ֵ,ֻҪ�f(shu��)�� ����Сֵ����ڵ���0����.��֪����(sh��)��һ��(g��)�^(q��)�g�ϵĆ��{(di��o)��,���D(zhu��n)���錧(d��o)����(sh��)���@��(g��)�^(q��)�g�Ϻ������ؓ(f��)��(w��n)�},׃?y��u)�һ��(g��)�������(w��n)�},��������(y��ng)����(sh��)�����w��ֵ��(l��i)���C,����(sh��)�������Բ��ó���(sh��)���x��.
����Сֵ����ڵ���0����.��֪����(sh��)��һ��(g��)�^(q��)�g�ϵĆ��{(di��o)��,���D(zhu��n)���錧(d��o)����(sh��)���@��(g��)�^(q��)�g�Ϻ������ؓ(f��)��(w��n)�},׃?y��u)�һ��(g��)�������(w��n)�},��������(y��ng)����(sh��)�����w��ֵ��(l��i)���C,����(sh��)�������Բ��ó���(sh��)���x��.
ԇ�}��������1�����}�⣺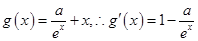
�ٮ�(d��ng) �r(sh��)��
�r(sh��)�� ��
�� ��
�� �ϵ�������(sh��)������
�ϵ�������(sh��)������ �o(w��)�Oֵ��
�o(w��)�Oֵ��
�ڮ�(d��ng) �r(sh��)����
�r(sh��)���� �ã�
�ã�
 ��
�� ��
�� ��
��
���� ��
�� �φ��{(di��o)�f�p����
�φ��{(di��o)�f�p���� �φ��{(di��o)�f��
�φ��{(di��o)�f��
���� ��
�� ̎ȡ�ØOСֵ���ҘOСֵ��
̎ȡ�ØOСֵ���ҘOСֵ�� ���o(w��)�O��ֵ
���o(w��)�O��ֵ
�C�ϣ���(d��ng) �r(sh��)��
�r(sh��)�� �o(w��)�Oֵ����(d��ng)
�o(w��)�Oֵ����(d��ng) ��
�� ��
�� ̎ȡ�ØOСֵ
̎ȡ�ØOСֵ ���o(w��)�O��ֵ��
���o(w��)�O��ֵ��
��2����
�O(sh��) ���t
���t
���� �r(sh��)��
�r(sh��)�� ��
�� �r(sh��)��
�r(sh��)��
���� ��
�� �φ��{(di��o)�f�p,��
�φ��{(di��o)�f�p,�� �φ��{(di��o)�f��,
�φ��{(di��o)�f��,
����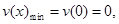 ��
�� ��
�� �φ��{(di��o)�f��.
�φ��{(di��o)�f��.
���c(di��n)��1������(sh��)�ĘOֵ��ֵ��2����(g��u)�캯��(sh��)��Q��(w��n)�}.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪x��3�Ǻ���(sh��)f(x)��aln(1��x)��x2��10x��һ��(g��)�Oֵ�c(di��n)��
(1)��a��
(2)��(sh��)f(x)���{(di��o)�^(q��)�g��
(3)��ֱ��y��b�c����(sh��)y��f(x)�ĈD����3��(g��)���c(di��n)����b��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��) �ĈD�����c(di��n)
�ĈD�����c(di��n) ̎���о�б�ʞ�10.
̎���о�б�ʞ�10.
(1)��(sh��)��(sh��) ��ֵ;
��ֵ;
(2)�Д��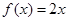 ���Ă�(g��)��(sh��),���C����ĽY(ji��)Փ;
���Ă�(g��)��(sh��),���C����ĽY(ji��)Փ;
(21)̽��: �Ƿ�����@�ӵ��c(di��n) ,ʹ������
,ʹ������ ��ԓ�c(di��n)���������҃ɲ��ַքeλ��������ԓ�c(di��n)̎�о��ăɂ�(c��)? ������,����c(di��n)A������(bi��o);��������,�f(shu��)������.
��ԓ�c(di��n)���������҃ɲ��ַքeλ��������ԓ�c(di��n)̎�о��ăɂ�(c��)? ������,����c(di��n)A������(bi��o);��������,�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��)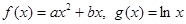 ��
��
��(d��ng)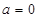 �r(sh��)������
�r(sh��)������ �ĈD���c
�ĈD���c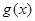 �ĈD���������c(di��n)
�ĈD���������c(di��n)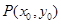 ����
����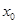 ��
�� ��ֵ��
��ֵ��
��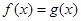 ��
��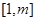 ���н⣬��
���н⣬�� �ķ�����
�ķ�����
�Ʈ�(d��ng)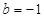 �r(sh��)����
�r(sh��)����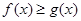 ��
��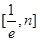 �Ϻ��������
�Ϻ�������� ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)����(sh��)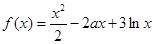
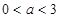 .
.
��1����(d��ng)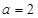 �r(sh��)����(sh��)
�r(sh��)����(sh��)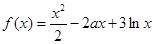 ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2����(d��ng)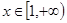 �r(sh��)����
�r(sh��)����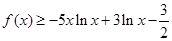 ���������
��������� ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪ �D���^(gu��)�c(di��n)
�D���^(gu��)�c(di��n) ������
������ ̎���о�������
̎���о������� .
.
��1���� �Ľ���ʽ��
�Ľ���ʽ��
��2���� �څ^(q��)�g
�څ^(q��)�g �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��) ������
������ .
.
������ ����(sh��)
����(sh��) �ĘOֵ�c(di��n)��
�ĘOֵ�c(di��n)��
������ �څ^(q��)�g
�څ^(q��)�g ��(n��i)���{(di��o)�f������(sh��)��(sh��)
��(n��i)���{(di��o)�f������(sh��)��(sh��)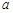 ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D���F(xi��n)Ҫ��߅�L(zh��ng)�� ��������
�������� ��(n��i)��һ��(g��)��ͨ���h(hu��n)�u��.�����ε��Ă�(g��)��c(di��n)��A�����Ă�(g��)�Ƿքe���돽��
��(n��i)��һ��(g��)��ͨ���h(hu��n)�u��.�����ε��Ă�(g��)��c(di��n)��A�����Ă�(g��)�Ƿքe���돽�� ��
�� ����
��С��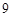 �������λ������������ε����Ğ�A�Ľ�һ��(g��)�돽��
�������λ������������ε����Ğ�A�Ľ�һ��(g��)�돽�� �ĈA�βݵ�.���˱��C��·��ͨ���u�ڌ���С��
�ĈA�βݵ�.���˱��C��·��ͨ���u�ڌ���С�� ���@�u����·������С��
���@�u����·������С�� .
.
��1���� ��ȡֵ���������\(y��n)����
��ȡֵ���������\(y��n)���� ȡ
ȡ ��
��
��2�������g�ݵص���r(ji��)�� Ԫ
Ԫ ���Ă�(g��)��������r(ji��)��
���Ă�(g��)��������r(ji��)�� Ԫ
Ԫ �������^(q��)�����r(ji��)��
�������^(q��)�����r(ji��)�� Ԫ
Ԫ ����(d��ng)
����(d��ng) ȡ��ֵ�r(sh��)����ʹ���h(hu��n)�u�������w��r(ji��)��ͣ�
ȡ��ֵ�r(sh��)����ʹ���h(hu��n)�u�������w��r(ji��)��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪����(sh��) ������
������ �鳣��(sh��).
�鳣��(sh��).
����������(sh��) �Dž^(q��)�g
�Dž^(q��)�g �ϵ�������(sh��)����(sh��)��(sh��)
�ϵ�������(sh��)����(sh��)��(sh��) ��ȡֵ������
��ȡֵ������
������ ��
�� �r(sh��)���������(sh��)��(sh��)
�r(sh��)���������(sh��)��(sh��) ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com