
【題目】已知多面體![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點。
的中點。
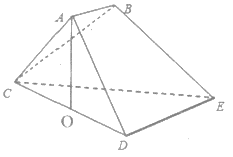
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求異面直線![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(Ⅰ)證明見解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)取CE中點F,連接BF,OF,由幾何關系可證得四邊形ABFO為平行四邊形,結合線面平行的性質定理可得題中的結論;
(Ⅱ)取DE中點M,連接AF,由題意可證得ABEM為平行四邊形,從而∠CAM或其補角為AC與BE所成的角.求得三角形的邊長,利用余弦定理可得異面直線AC和BE所成角的余弦值.
(Ⅲ)由題意結合(Ⅱ)中的結論可知∠DBF就是直線BD與平面BEC所成角,利用邊長的比值關系可得![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
(Ⅰ)取CE中點F,連接BF,OF,
∵O為CD的中點,
∴OF∥DE,且OF=DE,
∵AB//DE,AC=AD=CD=DE=2,AB=1,
∴OF∥AB,OF=AB,
則四邊形ABFO為平行四邊形,
∴AO//BF,BF平面BCE,AO平面BCE,
∴AO//平面BCE;
(Ⅱ)取DE中點M,連接AF,
∵AB∥DE,AB=1,DE=2,
∴AB∥ME,AB=ME ,
∴ABEM為平行四邊形.
∴AM//BE.
∴∠CAM或其補角為AC與BE所成的角.
∵DE⊥平面ACD,AD,CD平面ACD,
∴DE⊥CD,DE⊥AD,
在![]() 中,CD=2,DM=1,
中,CD=2,DM=1,![]() ,
,
在![]() 中,AD=2,DM=1,
中,AD=2,DM=1,![]() ,
,
![]() .
.
所以異面直線AC和BE所成角的余弦值為![]() .
.
(Ⅲ)由題意可得BF//AO,
∵AO⊥平面CDE,∴BF⊥平面CDE,∴BF⊥DF.
∵CD=DE,∴DF⊥CE,
∵BF∩CE=F,∴DF⊥平面CBE;
∴∠DBF就是直線BD與平面BEC所成角.
在△BDF中,![]() ,
,
![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓與拋物線![]() 有一個相同的焦點,且該橢圓的離心率為
有一個相同的焦點,且該橢圓的離心率為![]() ,
,
(Ⅰ)求該橢圓的標準方程:
(Ⅱ)求過點![]() 的直線與該橢圓交于A,B兩點,O為坐標原點,若
的直線與該橢圓交于A,B兩點,O為坐標原點,若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() 是正三角形,
是正三角形,![]() 為
為![]() 的中點,平面
的中點,平面![]() 平面
平面![]() .
.
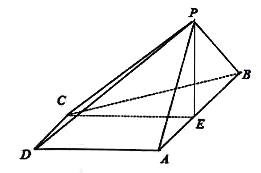
(1)求證:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n項和為Sn,等比數列{bn}的前n項和為Tn,a1=﹣1,b1=1,a2+b2=2.
(1)若a3+b3=5,求{bn}的通項公式;
(2)若T3=21,求S3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,以原點為圓心,橢圓的短半軸為半徑的圓與直線
,以原點為圓心,橢圓的短半軸為半徑的圓與直線![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() ,
,![]() ,
,![]() 是橢圓
是橢圓![]() 上關于
上關于![]() 軸對稱的任意兩個不同的點,連結
軸對稱的任意兩個不同的點,連結![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() ,證明:直線
,證明:直線![]() 與
與![]() 軸相交于定點
軸相交于定點![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的各項均為正數,
的各項均為正數,![]() ,且對任意
,且對任意![]() ,都有
,都有![]() ,數列
,數列![]() 前n項的和
前n項的和![]() .
.
(1)若數列![]() 是等比數列,求
是等比數列,求![]() 的值和
的值和![]() ;
;
(2)若數列![]() 是等差數列,求
是等差數列,求![]() 和
和![]() 的關系式;
的關系式;
(3)![]() ,當
,當![]() 時,求證:
時,求證: ![]() 是一個常數.
是一個常數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司新發明了甲、乙兩種不同型號的手機,公司統計了消費者對這兩種型號手機的評分情況,作出如下的雷達圖,則下列說法不正確的是( )
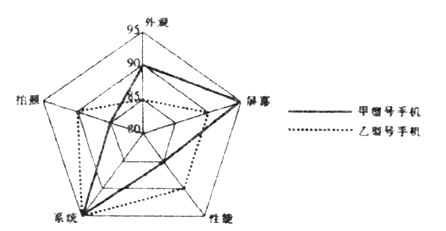
A. 甲型號手機在外觀方面比較好.B. 甲、乙兩型號的系統評分相同.
C. 甲型號手機在性能方面比較好.D. 乙型號手機在拍照方面比較好.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com