
【題目】已知極坐標系的極點與直角坐標系的原點重合,極軸與x軸的非負半軸重合,若曲線C1的方程為ρsin(θ+ ![]() )+2
)+2 ![]() =0,曲線C2的參數方程為
=0,曲線C2的參數方程為 ![]() (θ為參數).
(θ為參數).
(1)將C1的方程化為直角坐標方程;
(2)若點Q為C2上的動點,P為C1上的動點,求|PQ|的最小值.
 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:
【題目】某市為提高市民的戒煙意識,通過一個戒煙組織面向全市煙民征招志愿戒煙者,從符合條件的志愿者中隨機抽取100名,將年齡分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五組,得到頻率分布直方圖如圖所示.
五組,得到頻率分布直方圖如圖所示.

(1)求圖中![]() 的值,并估計這100名志愿者的平均年齡(同一組中的數據用該組區間的中點值作代表);
的值,并估計這100名志愿者的平均年齡(同一組中的數據用該組區間的中點值作代表);
(2)若年齡在![]() 的志愿者中有2名女性煙民,現從年齡在
的志愿者中有2名女性煙民,現從年齡在![]() 的志愿者中隨機抽取2人,求至少有一名女性煙民的概率;
的志愿者中隨機抽取2人,求至少有一名女性煙民的概率;
(3)該戒煙組織向志愿者推薦了![]() ,
,![]() 兩種戒煙方案,這100名志愿者自愿選取戒煙方案,并將戒煙效果進行統計如下:
兩種戒煙方案,這100名志愿者自愿選取戒煙方案,并將戒煙效果進行統計如下:
有效 | 無效 | 合計 | |
方案 | 48 | 60 | |
方案 | 36 | ||
合計 |
完成上面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為戒煙方案是否有效與方案選取有關.
的把握認為戒煙方案是否有效與方案選取有關.
參考公式:![]() ,
,![]() .
.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩地生產某種產品,他們可以調出的數量分別為300噸、750噸.A,B,C三地需要該產品數量分別為200噸,450噸,400噸,甲地運往A,B,C三地的費用分別為6元/噸、3元/噸,5元/噸,乙地運往A,B,C三地的費用分別為5元/噸,9元/噸,6元/噸,問怎樣調運,才能使總運費最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】東莞市公交公司為了方便廣大市民出行,科學規劃公交車輛的投放,計劃在某個人員密集流動地段增設一個起點站,為了研究車輛發車的間隔時間![]() 與乘客等候人數
與乘客等候人數![]() 之間的關系,選取一天中的六個不同的時段進行抽樣調查,經過統計得到如下數據:
之間的關系,選取一天中的六個不同的時段進行抽樣調查,經過統計得到如下數據:
間隔時間( | 8 | 10 | 12 | 14 | 16 | 18 |
等候人數( | 16 | 19 | 23 | 26 | 29 | 33 |
調查小組先從這6組數據中選取其中的4組數據求得線性回歸方程,再用剩下的2組數據進行檢驗,檢驗方法如下:先用求得的線性回歸方程計算間隔時間對應的等候人數![]() ,再求
,再求![]() 與實際等候人數
與實際等候人數![]() 的差,若兩組差值的絕對值均不超過1,則稱所求的回歸方程是“理想回歸方程”.
的差,若兩組差值的絕對值均不超過1,則稱所求的回歸方程是“理想回歸方程”.
參考公式:用最小二乘法求線性回歸方程![]() 的系數公式:
的系數公式: ,
,
(1)若選取的是前4組數據,求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)判斷(1)中的方程是否是“理想回歸方程”:
(3)為了使等候的乘客不超過38人,試用(1)中方程估計間隔時間最多可以設置為多少分鐘?
查看答案和解析>>
科目:高中數學 來源: 題型:
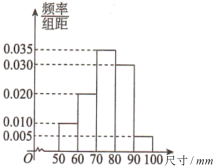
【題目】某工廠為檢驗車間一生產線工作是否正常,現從生產線中隨機抽取一批零件樣本,測量它們的尺寸(單位:![]() )并繪成頻率分布直方圖,如圖所示.根據長期生產經驗,可以認為這條生產線正常狀態下生產的零件尺寸
)并繪成頻率分布直方圖,如圖所示.根據長期生產經驗,可以認為這條生產線正常狀態下生產的零件尺寸![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為零件樣本平均數
近似為零件樣本平均數![]() ,
,![]() 近似為零件樣本方差
近似為零件樣本方差![]() .
.
(1)求這批零件樣本的![]() 和
和![]() 的值(同一組中的數據用該組區間的中點值作代表);
的值(同一組中的數據用該組區間的中點值作代表);
(2)假設生產狀態正常,求![]() ;
;
(3)若從生產線中任取一零件,測量其尺寸為![]() ,根據
,根據![]() 原則判斷該生產線是否正常?
原則判斷該生產線是否正常?
附:![]() ;若
;若![]() ,則
,則![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com