【題目】下列命題：
①若
是定義在
上的偶函數，且在
上是增函數，
，則
；
②若銳角
、
滿足c
，則
；
③若
，則
對
恒成立；
④要得到
的圖像，只需將
的圖像向右平移
個單位：
其中真命題的個數有（ ）
A.1B.2C.3D.4
每日10分鐘口算心算速算天天練系列答案科目：高中數學 來源： 題型：
【題目】甲、乙兩位學生參加數學競賽培訓．現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取
次．記錄如下：
甲： 
， 
， 
， 
， 
， 
， 
， 
乙： 
， 
， 
， 
， 
， 
， 
， 
（
）用莖葉圖表示這兩組數據．
（
）現要從中選派一人參加數學競賽，從統計學的角度考慮，你認為派哪位學生參加合適?請說明理由．
（
）若將頻率視為概率，對甲同學在今后的三次數學競賽成績進行預測，記這
次成績中高于
分的次數為
，求
的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若數列{an}是公差為2的等差數列，數列{bn}滿足b1＝1，b2＝2，且anbn＋bn＝nbn＋1.
(1)求數列{an}，{bn}的通項公式；
(2)設數列{cn}滿足
，數列{cn}的前n項和為Tn，若不等式(－1)nλ<Tn＋
對一切n∈N*恒成立，求實數λ的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】正△ABC的邊長為2, CD是AB邊上的高，E、F分別是AC和BC的中點(如圖(1))．現將△ABC沿CD翻成直二面角A－DC－B(如圖(2))．在圖(2)中：
(1)求證：AB∥平面DEF；
(2)在線段BC上是否存在一點P，使AP⊥DE？證明你的結論；
(3)求二面角E－DF－C的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平行六面體ABCD－A1B1C1D1中，AA1⊥平面ABCD，且AB＝AD＝2，AA1＝
，∠BAD＝120°.
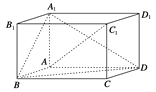
(1)求異面直線A1B與AC1所成角的余弦值；
(2)求二面角B－A1D－A的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若實數
，
滿足
，則
的最小值是（ ）
A. 0 B. 
C. -6 D. -3
【答案】C
【解析】
畫出可行域，向上平移目標函數
到可行域邊界的位置，由此求得目標函數的最小值.
畫出可行域如下圖所示，由圖可知，目標函數
在點
處取得最小值為
.故選C.
【點睛】
本小題主要考查線性規劃的知識，考查線性目標函數的最值的求法，考查數形結合的數學思想方法，屬于基礎題.畫可行域時，要注意判斷不等式所表示的范圍是在直線的哪個方位，不一定是三條直線圍成的三角形.還要注意目標函數化成斜截式后，截距和目標函數的對應關系，截距最大時，目標函數不一定取得最大值，可能取得最小值.
【題型】單選題
【結束】
12
【題目】已知
，
是橢圓
長軸上的兩個端點，
，
是橢圓上關于軸對稱的兩點，直線
，
的斜率分別為
，若橢圓的離心率為
，則
的最小值為（ ）
A. 1 B. 
C. 
D. 2
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校進行文科、理科數學成績對比，某次考試后，各隨機抽取100名同學的數學考試成績進行統計，其頻率分布表如下.
（Ⅰ）根據數學成績的頻率分布表，求理科數學成績的中位數的估計值；（精確到0.01）
（Ⅱ）請填寫下面的列聯表，并根據列聯表判斷是否有90%的把握認為數學成績與文理科有關：
參考公式與臨界值表： 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是正方體的平面展開圖，在這個正方體中，正確的命題是（ ）
A. BD與CF成60°角 B. BD與EF成60°角 C. AB與CD成60°角 D. AB與EF成60°角
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
