
【題目】已知函數f(x)=2sin(x+ ![]() )cosx.
)cosx.
(1)若0≤x≤ ![]() ,求函數f(x)的值域;
,求函數f(x)的值域;
(2)設△ABC的三個內角A,B,C所對的邊分別為a,b,c,若A為銳角且f(A)= ![]() ,b=2,c=3,求cos(A﹣B)的值.
,b=2,c=3,求cos(A﹣B)的值.
【答案】
(1)解:f(x)=2sin(x+ ![]() )cosx
)cosx
=(sinx+ ![]() cosx)cosx
cosx)cosx
=sinxcosx+ ![]() cos2x
cos2x
= ![]() sin2x+
sin2x+ ![]() cos2x+
cos2x+ ![]()
=sin(2x+ ![]() )+
)+ ![]() ;
;
由 ![]() 得,
得, ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
即函數f(x)的值域為 ![]()
(2)解:由 ![]() ,
,
得 ![]() ,
,
又由 ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,解得
,解得 ![]() ;
;
在△ABC中,由余弦定理a2=b2+c2﹣2bccosA=7,
解得 ![]() ;
;
由正弦定理 ![]() ,得
,得 ![]() ,
,
∵b<a,∴B<A,∴ ![]() ,
,
∴cos(A﹣B)=cosAcosB+sinAsinB
= ![]()
【解析】(1)利用三角恒等變換化簡f(x),根據x的取值范圍即可求出函數f(x)的值域;(2)由f(A)的值求出角A的大小,再利用余弦定理和正弦定理,即可求出cos(A﹣B)的值.
【考點精析】解答此題的關鍵在于理解余弦定理的定義的相關知識,掌握余弦定理:![]() ;
;![]() ;
;![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,且
為直角梯形,且![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 為
為![]() 的中點,
的中點, ![]() 是棱
是棱![]() 的中點,
的中點, ![]() ,
,![]() .
.


(1)求證:![]() 平面BDM; (2)D到面PBC距離;
平面BDM; (2)D到面PBC距離;
(3)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x﹣1|.
(1)若不等式f(x+ ![]() )≥2m+1(m>0)的解集為(﹣∞,﹣2]∪[2,+∞),求實數m的值;
)≥2m+1(m>0)的解集為(﹣∞,﹣2]∪[2,+∞),求實數m的值;
(2)若不等式f(x)≤2y+ ![]() +|2x+3|,對任意的實數x,y∈R恒成立,求實數a的最小值.
+|2x+3|,對任意的實數x,y∈R恒成立,求實數a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=3x+λ3﹣x(λ∈R).
(1)若f(x)為奇函數,求λ的值和此時不等式f(x)>1的解集;
(2)若不等式f(x)≤6對x∈[0,2]恒成立,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一塊平行四邊形綠地ABCD,經測量BC=2百米,CD=1百米,∠BCD=120°,擬過線段BC上一點E設計一條直路EF(點F在四邊形ABCD的邊上,不計路的寬度),將綠地分為面積之比為1:3的左右兩部分,分別種植不同的花卉,設EC=x百米,EF=y百米. 
(1)當點F與點D重合時,試確定點E的位置;
(2)試求x的值,使路EF的長度y最短.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司對新招聘的員工張某進行綜合能力測試,共設置了A,B,C三個測試項目.假定張某通過項目A的概率為 ![]() ,通過項目B,C的概率均為a(0<a<1),且這三個測試項目能否通過相互獨立.
,通過項目B,C的概率均為a(0<a<1),且這三個測試項目能否通過相互獨立.
(1)用隨機變量X表示張某在測試中通過的項目個數,求X的概率分布和數學期望E(X)(用a表示);
(2)若張某通過一個項目的概率最大,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
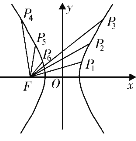
【題目】如圖所示,F為雙曲線C:![]() ﹣
﹣![]() =1的左焦點,雙曲線C上的點Pi與P7﹣i(i=1,2,3)關于y軸對稱,則|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
=1的左焦點,雙曲線C上的點Pi與P7﹣i(i=1,2,3)關于y軸對稱,則|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
A. 9 B. 16 C. 18 D. 27
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A、B為拋物線C:![]() 上兩點,A與B的中點的橫坐標為2,直線AB的斜率為1.
上兩點,A與B的中點的橫坐標為2,直線AB的斜率為1.
(Ⅰ)求拋物線C的方程;
(Ⅱ)直線![]() 交x軸于點M,交拋物線C:
交x軸于點M,交拋物線C:![]() 于點P,M關于點P的對稱點為N,連結ON并延長交C于點H.除H以外,直線MH與C是否有其他公共點?請說明理由.
于點P,M關于點P的對稱點為N,連結ON并延長交C于點H.除H以外,直線MH與C是否有其他公共點?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com