【題目】函數
.
（1）當
時，討論函數
的單調性；
（2）當
時，
時，
恒成立，求正整數
的最大值.
【答案】（1）見解析
（2）
【解析】
（1）對
求導，再因式分解，討論每個因式的正負，再判斷
的正負，進而判斷的單調性；（2）代入
，將不等式
中的
和
分離在不等號兩邊，然后討論不等號含有一邊的函數的單調性，進而判斷最值，再計算的取值范圍，由是正整數的條件可求出的最大值.
解：（1）函數的定義域為
，
①當
時，因為
，故有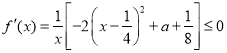
.
此時函數在區間單調遞減.
②當
，有
，方程
的兩根分別是：
函數
在
上單調遞減；
當
函數在
上單調遞增；
當
函數在
上單調遞減.
③當
時，易知在
上單調遞增，在
上單調遞減.
綜上所述，當時，在上單調遞減；
當時，在
上單調遞減，
在
上單調遞增；
當時，在上單調遞增，在單調遞減.
（2）當
設
當
時，有
，
設
在
上單調遞增，
又
在
上的函數圖像是一條不間斷的曲線，
且
，
存在唯一的
，使得
，即
.
當
；
當
，
在
上單調遞減，在
上單調遞增，
在
上單調遞減，
，
時，不等式
對任意
恒成立，
正整數的最大值是3.
科目：高中數學 來源： 題型：
【題目】為了解運動健身減肥的效果，某健身房調查了20名肥胖者，測量了他們的體重（單位：千克）．健身之前他們的體重情況如三維餅圖（1）所示，經過半年的健身后，他們的體重情況如三維餅圖（2）所示，對比健身前后，關于這20名肥胖者，下面結論正確的是（ ）
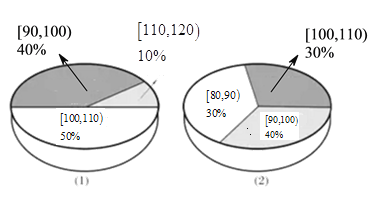
A.他們健身后，體重在區間
內的人數不變
B.他們健身后，體重在區間
內的人數減少了2個
C.他們健身后，體重在區間
內的肥胖者體重都有減輕
D.他們健身后，這20位肥胖著的體重的中位數位于區間
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圖1是某高架橋箱梁的橫截面，它由上部路面和下部支撐箱兩部分組成．如圖2，路面寬度
，下部支撐箱CDEF為等腰梯形（
），且
．為了保證承重能力與穩定性，需下部支撐箱的面積為
，高度為2m且
，若路面AB．側邊CF和DE，底部EF的造價分別為4a千元/m，5a千元/m，6a千元/m（a為正常數），
．
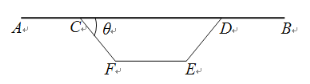
（1）試用θ表示箱梁的總造價y（千元）；
（2）試確定cosθ的值，使總造價最低?并求最低總造價．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】斜率為
的直線
過拋物線
的焦點
，且與拋物線
交于
、
兩點.
（1）設點在第一象限，過作拋物線的準線的垂線，
為垂足，且
，直線
與直線關于直線
對稱，求直線的方程；
（2）過且與垂直的直線
與圓
交于
、
兩點，若
與
面積之和為
，求的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】斜率為
的直線
過拋物線
：
的焦點
，且與拋物線交于
，
兩點．
（1）設點在笫一象限，過作拋物線的準線的垂線，
為垂足，且
，求點的坐標；
（2）過且與垂直的直線
與圓
：
交于
，
兩點，若
與
面積之和為
，求的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，某中學甲、乙兩班共有25名學生報名參加了一項 測試．這25位學生的考分編成的莖葉圖，其中有一個數據因電腦操作員不小心刪掉了（這里暫用x來表示），但他清楚地記得兩班學生成績的中位數相同．
（Ⅰ）求這兩個班學生成績的中位數及x的值；
（Ⅱ）如果將這些成績分為“優秀”（得分在175分 以上，包括175分）和“過關”，若學校再從這兩個班獲得“優秀”成績的考生中選出3名代表學校參加比賽，求這3人中甲班至多有一人入選的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
