
【題目】![]() 的內(nèi)角
的內(nèi)角![]() 的對(duì)邊分別為
的對(duì)邊分別為![]() ,且
,且![]() .
.
(1)證明: ![]() 成等比數(shù)列;
成等比數(shù)列;
(2)若角![]() 的平分線
的平分線![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,且
,且![]() ,求
,求![]() .
.
【答案】(1)見(jiàn)解析;(2)![]() .
.
【解析】試題分析:(1)利用兩角和的余弦函數(shù)公式化簡(jiǎn)已知等式可得sinAsinC=sin2B,由正弦定理可得:b2=ac,即可得證.(2)由已知可得:AD+CD=6,由三角形面積公式可得AD=2CD,從而可求AD=4,CD=2,由(1)可得:b2=36,利用角平分線的性質(zhì)可得AB=2BC,即c=2a,從而可求a,c的值,進(jìn)而利用余弦定理可求cosA,即可由余弦定理求得BD的值.
試題解析:.解法一:
(1)因?yàn)?/span>![]() ,
,
所以![]() ,
,
化簡(jiǎn)可得![]() ,
,
由正弦定理得, ![]() ,故
,故![]() 成等比數(shù)列.
成等比數(shù)列.
(2)由題意![]() ,得
,得![]() ,
,
又因?yàn)?/span>![]() 是角平分線,所以
是角平分線,所以![]() ,即
,即![]() ,
,
化簡(jiǎn)得, ![]() ,即
,即![]() .
.
由(1)知, ![]() ,解得
,解得![]() ,
,
再由![]() 得,
得, ![]() (
(![]() 為
為![]() 中
中![]() 邊上的高),
邊上的高),
即![]() ,又因?yàn)?/span>
,又因?yàn)?/span>![]() ,所以
,所以![]() .
.
【注】利用角平分線定理得到![]() 同樣得分,
同樣得分,
在![]() 中由余弦定理可得,
中由余弦定理可得, ![]() ,
,
在![]() 中由余弦定理可得,
中由余弦定理可得, ![]() ,
,
即![]() ,求得
,求得![]() .
.
解法二:(1)同解法一.
(2)同解法一, ![]() .
.
在![]() 中由余弦定理可得,
中由余弦定理可得, ![]() ,
,
在![]() 中由余弦定理可得,
中由余弦定理可得, ![]() ,
,
即![]() ,求得
,求得![]() .
.
解法三:
(1)同解法一.
(2)同解法二, ![]() .
.
在![]() 中由余弦定理可得,
中由余弦定理可得, ![]() ,
,
由于![]() ,從而可得
,從而可得![]() ,
,
在![]() 中由余弦定理可得,
中由余弦定理可得, ![]() ,求得
,求得![]() ,
,
在![]() 中由正弦定理可得,
中由正弦定理可得, ![]() ,即
,即![]() .
.
【注】若求得![]() 的值后,在
的值后,在![]() 中應(yīng)用正弦定理求得
中應(yīng)用正弦定理求得![]() 的,請(qǐng)類(lèi)比得分.
的,請(qǐng)類(lèi)比得分.
解法四:
(1)同解法一.
(2)同解法一, ![]() .
.
在![]() 中由余弦定理得,
中由余弦定理得, 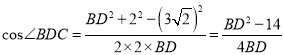 ,
,
在![]() 中由余弦定理得,
中由余弦定理得, 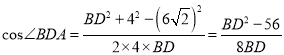 ,
,
因?yàn)?/span>![]() ,所以有
,所以有![]() ,
,
故![]() ,
,
整理得, ![]() ,即
,即![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公司制定了一個(gè)激勵(lì)銷(xiāo)售人員的獎(jiǎng)勵(lì)方案:當(dāng)銷(xiāo)售利潤(rùn)不超過(guò)15萬(wàn)元時(shí),按銷(xiāo)售利潤(rùn)的10%進(jìn)行獎(jiǎng)勵(lì);當(dāng)銷(xiāo)售利潤(rùn)超過(guò)15萬(wàn)元時(shí),若超過(guò)部分為A萬(wàn)元,則超出部分按2log5(A+1)進(jìn)行獎(jiǎng)勵(lì),沒(méi)超出部分仍按銷(xiāo)售利潤(rùn)的10%進(jìn)行獎(jiǎng)勵(lì).記獎(jiǎng)金總額為y(單位:萬(wàn)元),銷(xiāo)售利潤(rùn)為x(單位:萬(wàn)元).
(1)寫(xiě)出該公司激勵(lì)銷(xiāo)售人員的獎(jiǎng)勵(lì)方案的函數(shù)表達(dá)式;
(2)如果業(yè)務(wù)員老張獲得5.5萬(wàn)元的獎(jiǎng)金,那么他的銷(xiāo)售利潤(rùn)是多少萬(wàn)元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知過(guò)拋物線y2=2px(p>0)的焦點(diǎn)的直線交拋物線于A、B兩點(diǎn),且|AB|= ![]() p,求AB所在的直線方程.
p,求AB所在的直線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知 ![]() =(1,2),
=(1,2), ![]() =(﹣3,2),當(dāng)k為何值時(shí),
=(﹣3,2),當(dāng)k為何值時(shí),
(1)k ![]() 與
與 ![]() 垂直?
垂直?
(2)k ![]() 與
與 ![]() 夾角為鈍角?
夾角為鈍角?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
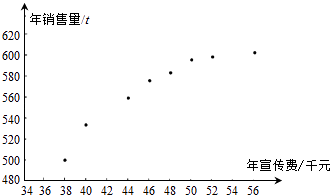
【題目】某公司為確定下一年度投入某種產(chǎn)品的宣傳費(fèi),需了解年宣傳費(fèi)x(單位:千元)對(duì)年銷(xiāo)售量y(單位:t)和年利潤(rùn)z(單位:千元)的影響.對(duì)近8年的年宣傳費(fèi)xi和年銷(xiāo)售量yi(i=1,2,,8)數(shù)據(jù)作了初步處理, 得到下面的散點(diǎn)圖及一些統(tǒng)計(jì)量的值.
| | | | | | |
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
其中wi= ![]() ,
, ![]() =
= ![]()
(Ⅰ)根據(jù)散點(diǎn)圖判斷,y=a+bx與y=c+d ![]() 哪一個(gè)適宜作為年銷(xiāo)售量y關(guān)于年宣傳費(fèi)x的回歸方程類(lèi)型?(給出判斷即可,不必說(shuō)明理由)
哪一個(gè)適宜作為年銷(xiāo)售量y關(guān)于年宣傳費(fèi)x的回歸方程類(lèi)型?(給出判斷即可,不必說(shuō)明理由)
(Ⅱ)根據(jù)(Ⅰ)的判斷結(jié)果及表中數(shù)據(jù),建立y關(guān)于x的回歸方程;
(Ⅲ)已知這種產(chǎn)品的年利潤(rùn)z與x、y的關(guān)系為z=0.2y﹣x.根據(jù)(Ⅱ)的結(jié)果回答下列問(wèn)題:
(i)年宣傳費(fèi)x=49時(shí),年銷(xiāo)售量及年利潤(rùn)的預(yù)報(bào)值是多少?
(ii)年宣傳費(fèi)x為何值時(shí),年利潤(rùn)的預(yù)報(bào)值最大?
附:對(duì)于一組數(shù)據(jù)(u1 , v1),(u2 , v2),,(un , vn),其回歸直線v=α+βμ的斜率和截距的最小二乘估計(jì)分別為: ![]() =
= 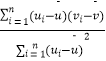 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】![]() 中,
中, ![]() 是
是![]() 的中點(diǎn),
的中點(diǎn), ![]() ,其周長(zhǎng)為
,其周長(zhǎng)為![]() ,若點(diǎn)
,若點(diǎn)![]() 在線段
在線段![]() 上,且
上,且![]() .
.
(1)建立合適的平面直角坐標(biāo)系,求點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若![]() 是射線
是射線![]() 上不同兩點(diǎn),
上不同兩點(diǎn), ![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 的直線與
的直線與![]() 交于
交于![]() ,直線
,直線![]() 與
與![]() 交于另一點(diǎn)
交于另一點(diǎn)![]() .證明:
.證明: ![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 有兩個(gè)不同的零點(diǎn).
有兩個(gè)不同的零點(diǎn).
(1)求![]() 的取值范圍;
的取值范圍;
(2)記兩個(gè)零點(diǎn)分別為![]() ,且
,且![]() ,已知
,已知![]() ,若不等式
,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)= ![]() ,x∈R.
,x∈R.
(1)分別求出f(2)+f( ![]() ),f(3)+f(
),f(3)+f( ![]() ),f(4)+f(
),f(4)+f( ![]() )的值;
)的值;
(2)根據(jù)(1)歸納猜想出f(x)+f( ![]() )的值,并證明.
)的值,并證明.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com