
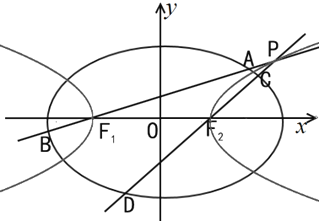
【題目】如圖,橢圓![]() 的左右焦點
的左右焦點![]() 、
、![]() 恰好是等軸雙曲線
恰好是等軸雙曲線![]() 的左右頂點,且橢圓的離心率為
的左右頂點,且橢圓的離心率為![]() ,
,![]() 是雙曲線
是雙曲線![]() 上異于頂點的任意一點,直線
上異于頂點的任意一點,直線![]() 和
和![]() 與橢圓的交點分別記為
與橢圓的交點分別記為![]() 、
、![]() 和
和![]() 、
、![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,求證:
,求證:![]() 為定值;
為定值;
(3)若存在點![]() 滿足
滿足![]() ,試求
,試求![]() 的大小.
的大小.
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右兩個焦點分別為
的左、右兩個焦點分別為![]() ,離心率
,離心率![]() ,短軸長為2.
,短軸長為2.
(1)求橢圓的方程;
(2)點![]() 為橢圓上的一動點(非長軸端點),
為橢圓上的一動點(非長軸端點),![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,
點, ![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,求
點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,以O為極點,x軸的正半軸為極軸建立極坐標系![]() 的極坐標方程為
的極坐標方程為![]() ,直線l的參數方程為
,直線l的參數方程為![]() ,(其中
,(其中![]() 為參數)直線l與
為參數)直線l與![]() 交于A,B兩個不同的點.
交于A,B兩個不同的點.
![]() 求傾斜角
求傾斜角![]() 的取值范圍;
的取值范圍;
![]() 求線段AB中點P的軌跡的參數方程.
求線段AB中點P的軌跡的參數方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
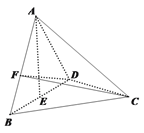
【題目】如圖,在三棱錐![]() 中,已知
中,已知![]() 都是邊長為
都是邊長為![]() 的等邊三角形,
的等邊三角形,![]() 為
為![]() 中點,且
中點,且![]() 平面
平面![]() ,
,![]() 為線段
為線段![]() 上一動點,記
上一動點,記![]() .
.
(1)當![]() 時,求異面直線
時,求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(2)當![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】制訂投資計劃時,不僅要考慮可能獲得的盈利,而且要考慮可能出現的虧損.某投資人打算投資甲、乙兩個項目.根據預測,甲、乙項目可能的最大盈利分別為![]() 和
和![]() ,可能的最大虧損率分別為
,可能的最大虧損率分別為![]() 和
和![]() .投資人計劃投資金額不超過
.投資人計劃投資金額不超過![]() 億元,要求確保可能的資金虧損不超過
億元,要求確保可能的資金虧損不超過![]() 億元,問投資人對甲、乙兩個項目各投資多少億元,才能使可能的盈利最大?
億元,問投資人對甲、乙兩個項目各投資多少億元,才能使可能的盈利最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的上頂點為A,右頂點為B.已知
的上頂點為A,右頂點為B.已知![]() (O為原點).
(O為原點).
(1)求橢圓的離心率;
(2)設點![]() ,直線
,直線![]() 與橢圓交于兩個不同點M,N,直線AM與x軸交于點E,直線AN與x軸交于點F,若
與橢圓交于兩個不同點M,N,直線AM與x軸交于點E,直線AN與x軸交于點F,若![]() .求證:直線l經過定點.
.求證:直線l經過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com