
【題目】如圖,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中點,則圖中直角三角形的個數(shù)是 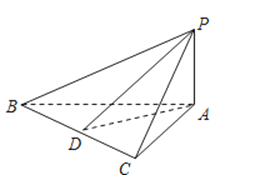
【答案】8
【解析】解:在Rt△ABC中,∠BAC=90°,
PA⊥平面ABC,
∴AB⊥PA,PA⊥DA,PA⊥AC,
∵AB=AC,D是BC的中點,
∴AD⊥BC,
∴BP=CP,可得PD⊥BC,
∴圖中直角三角形有△PAC,△PAB,△PAD,△ABC.△ABD,△ADC,△BPD,△DPC,8個.
所以答案是:8.
【考點精析】解答此題的關鍵在于理解直線與平面垂直的判定的相關知識,掌握一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現(xiàn)了“直線與平面垂直”與“直線與直線垂直”互相轉化的數(shù)學思想.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 在區(qū)間
在區(qū)間![]() 上單調遞增,求實數(shù)
上單調遞增,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若存在唯一整數(shù)![]() ,使得
,使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,棱柱ABC﹣A1B1C1的側面BCC1B1是菱形,B1C⊥A1B 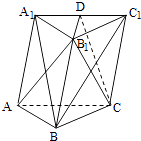
(1)證明:平面AB1C⊥平面A1BC1;
(2)設D是A1C1上的點,且A1B∥平面B1CD,求A1D:DC1的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,正方體![]() 的棱長為
的棱長為![]() ,
,![]() ,
,![]() 分別是棱
分別是棱![]() ,
,![]() 的中點,過直線
的中點,過直線![]() ,
,![]() 的平面分別與棱
的平面分別與棱![]() 、
、![]() 交于
交于![]() ,
,![]() ,設
,設![]() ,
,![]() ,給出以下四個命題:
,給出以下四個命題:
①平面![]() 平面
平面![]() ;
;
②當且僅當![]() 時,四邊形
時,四邊形![]() 的面積最小;
的面積最小;
③四邊形![]() 周長
周長![]() ,
,![]() 是單調函數(shù);
是單調函數(shù);
④四棱錐![]() 的體積
的體積![]() 為常函數(shù);
為常函數(shù);
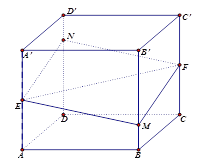
以上命題中假命題的序號為( ).
A. ①④ B. ② C. ③ D. ③④
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且滿足![]() .
.
(1)求角B的大小;
(2)若點M為BC中點,且AM=AC=2,求a的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在2016年龍巖市初中體育中考中,隨意抽取某校5位同學一分鐘跳繩的次數(shù)分別為:158,160,154,158,170,則由這組數(shù)據(jù)得到的結論錯誤的是( )
A.平均數(shù)為160
B.中位數(shù)為158
C.眾數(shù)為158
D.方差為20.3
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com