
【題目】已知點![]() ,⊙
,⊙![]() .
.
(Ⅰ)當直線![]() 過點
過點![]() 且與圓心
且與圓心![]() 的距離為
的距離為![]() 時,求直線
時,求直線![]() 的方程.
的方程.
(Ⅱ)設過點![]() 的直線與⊙
的直線與⊙![]() 交于
交于![]() ,
, ![]() 兩點,且
兩點,且![]() ,求以線段
,求以線段![]() 為直徑的圓的方程.
為直徑的圓的方程.
 教學練新同步練習系列答案
教學練新同步練習系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Tn= ![]() n2﹣
n2﹣ ![]() n,且an+2+3log4bn=0(n∈N*)
n,且an+2+3log4bn=0(n∈N*)
(1)求{bn}的通項公式;
(2)數列{cn}滿足cn=anbn , 求數列{cn}的前n項和Sn;
(3)若cn≤ ![]() m2+m﹣1對一切正整數n恒成立,求實數m的取值范圍.
m2+m﹣1對一切正整數n恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著人口老齡化的到來,我國的勞動力人口在不斷減少,“延遲退休”已經成為人們越來越關注的話題,為了解公眾對“延遲退休”的態度,某校課外研究性學習小組在某社區隨機抽取了50人進行調查,將調查情況進行整理后制成下表:
年齡 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人數 | 4 | 5 | 8 | 5 | 3 |
年齡 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人數 | 6 | 7 | 3 | 5 | 4 |
經調查年齡在[25,30),[55,60)的被調查者中贊成“延遲退休”的人數分別是3人和2人.現從這兩組的被調查者中各隨機選取2人,進行跟蹤調查.
(I)求年齡在[25,30)的被調查者中選取的2人都贊成“延遲退休”的概率;
(II)若選中的4人中,不贊成“延遲退休”的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程是
的參數方程是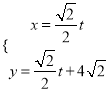 (
(![]() 是參數),以坐標原點為原點,
是參數),以坐標原點為原點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)判斷直線![]() 與曲線
與曲線![]() 的位置關系;
的位置關系;
(2)過直線![]() 上的點作曲線
上的點作曲線![]() 的切線,求切線長的最小值.
的切線,求切線長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 和直線
和直線![]() ,直線
,直線![]() ,
, ![]() 都經過圓
都經過圓![]() 外定點
外定點![]() .
.
(1)若直線![]() 與圓
與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,與
兩點,與![]() 交于
交于![]() 點,且線段
點,且線段![]() 的中點為
的中點為![]() ,
,
求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
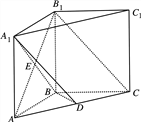
【題目】如圖,在直三棱柱ABC—A1B1C1中,AB=BC=BB1, ![]() ,D為AC上的點,B1C∥平面A1BD;
,D為AC上的點,B1C∥平面A1BD;
(1)求證:BD⊥平面![]() ;
;
(2)若![]() 且
且![]() ,求三棱錐A-BCB1的體積.
,求三棱錐A-BCB1的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段圖象如圖所示. 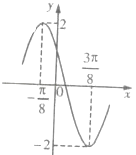
(1)求函數f(x)的解析式;
(2)求函數f(x)的單調增區間;
(3)求函數f(x)在[﹣ ![]() ,
, ![]() ]上的單調減區間.
]上的單調減區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com