
【題目】(本小題滿分16分)已知![]() 為實數,函數
為實數,函數![]() ,函數
,函數![]() .
.
(1)當![]() 時,令
時,令![]() ,求函數
,求函數![]() 的極值;
的極值;
(2)當![]() 時,令
時,令![]() ,是否存在實數
,是否存在實數![]() ,使得對于函數
,使得對于函數![]() 定義域中的任意實數
定義域中的任意實數![]() ,均存在實數
,均存在實數![]() ,有
,有![]() 成立,若存在,求出實數
成立,若存在,求出實數![]() 的取值集合;若不存在,請說明理由.
的取值集合;若不存在,請說明理由.
【答案】(1)![]() 的極小值為
的極小值為![]() ,無極大值.(2)
,無極大值.(2)![]()
【解析】試題分析:(1)當![]() 時,
時, ![]() ,定義域為
,定義域為![]() ,由
,由![]() 得
得![]() .列表分析得
.列表分析得![]() 的極小值為
的極小值為![]() ,無極大值.(2)恒成立問題及存在問題,一般利用最值進行轉化:
,無極大值.(2)恒成立問題及存在問題,一般利用最值進行轉化: ![]() 在
在![]() 上恒成立.由于
上恒成立.由于![]() 不易求,因此再進行轉化:當
不易求,因此再進行轉化:當![]() 時,
時, ![]() 可化為
可化為![]() ,令
,令![]() ,問題轉化為:
,問題轉化為: ![]() 對任意
對任意![]() 恒成立;同理當
恒成立;同理當![]() 時,
時, ![]() 可化為
可化為![]() ,令
,令![]() ,問題轉化為:
,問題轉化為: ![]() 對任意的
對任意的![]() 恒成立;以下根據導函數零點情況進行討論即可.
恒成立;以下根據導函數零點情況進行討論即可.
試題解析:(1)![]() ,
,
![]() ,令
,令![]() ,得
,得![]() . 1分
. 1分
列表:
x |
|
|
|
|
| 0 | + |
| ↘ | 極小值 | ↗ |
所以![]() 的極小值為
的極小值為![]() ,無極大值. 4分
,無極大值. 4分
(2)當![]() 時,假設存在實數
時,假設存在實數![]() 滿足條件,則
滿足條件,則![]() 在
在![]() 上恒成立. 5分
上恒成立. 5分
1)當![]() 時,
時, ![]() 可化為
可化為![]() ,
,
令![]() ,問題轉化為:
,問題轉化為: ![]() 對任意
對任意![]() 恒成立;(*)
恒成立;(*)
則![]() ,
, ![]() ,
, ![]() .
.
令![]() ,則
,則![]() .
.
①![]() 時,因為
時,因為![]() ,
,
故![]() ,所以函數
,所以函數![]() 在
在![]() 時單調遞減,
時單調遞減, ![]() ,
,
即![]() ,從而函數
,從而函數![]() 在
在![]() 時單調遞增,故
時單調遞增,故![]() ,所以(*)
,所以(*)
成立,滿足題意; 7分
②當![]() 時,
時, 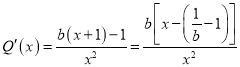 ,
,
因為![]() ,所以
,所以![]() ,記
,記![]() ,則當
,則當![]() 時,
時, ![]() ,
,
故![]() ,所以函數
,所以函數![]() 在
在![]() 時單調遞增,
時單調遞增, ![]() ,
,
即![]() ,從而函數
,從而函數![]() 在
在![]() 時單調遞減,所以
時單調遞減,所以![]() ,此時(*)不成立;
,此時(*)不成立;
所以當![]() ,
, ![]() 恒成立時,
恒成立時, ![]() ; 9分
; 9分
2)當![]() 時,
時, ![]() 可化為
可化為![]() ,
,
令![]() ,問題轉化為:
,問題轉化為: ![]() 對任意的
對任意的![]() 恒成立;(**)
恒成立;(**)
則![]() ,
, ![]() ,
, ![]() .
.
令![]() ,則
,則![]() .
.
①![]() 時,
時, ![]() ,
,
故![]() ,所以函數
,所以函數![]() 在
在![]() 時單調遞增,
時單調遞增, ![]() ,
,
即![]() ,從而函數
,從而函數![]() 在
在![]() 時單調遞增,所以
時單調遞增,所以![]() ,此時(**)成立;11分
,此時(**)成立;11分
②當![]() 時,
時,
ⅰ)若![]() ,必有
,必有![]() ,故函數
,故函數![]() 在
在![]() 上單調遞減,所以
上單調遞減,所以![]() ,即
,即![]() ,從而函數
,從而函數![]() 在
在![]() 時單調遞減,所以
時單調遞減,所以![]() ,此時(**)不成立; 13分
,此時(**)不成立; 13分
ⅱ)若![]() ,則
,則![]() ,所以當
,所以當![]() 時,
時,
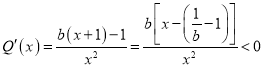 ,
,
故函數![]() 在
在![]() 上單調遞減,
上單調遞減, ![]() ,即
,即![]() ,所以函數
,所以函數![]() 在
在![]() 時單調遞減,所以
時單調遞減,所以![]() ,此時(**)不成立;
,此時(**)不成立;
所以當![]() ,
, ![]() 恒成立時,
恒成立時, ![]() ; 15分
; 15分
綜上所述,當![]() ,
, ![]() 恒成立時,
恒成立時, ![]() ,從而實數
,從而實數![]() 的取值集合為
的取值集合為![]() . 16分
. 16分


 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C的兩個焦點坐標分別是F1(﹣ ![]() ,0)、F2(
,0)、F2( ![]() ,0),并且經過點P(
,0),并且經過點P( ![]() ,﹣
,﹣ ![]() ).
).
(1)求橢圓C的方程;
(2)若直線l與圓O:x2+y2=1相切,并與橢圓C交于不同的兩點A、B.當 ![]() =λ,且滿足
=λ,且滿足 ![]() ≤λ≤
≤λ≤ ![]() 時,求△AOB面積S的取值范圍.
時,求△AOB面積S的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:對m∈[﹣1,1],不等式a2﹣5a﹣3≥ ![]() 恒成立;命題q:不等式x2+ax+2<0有解.若p是真命題,q是假命題,求a的取值范圍.
恒成立;命題q:不等式x2+ax+2<0有解.若p是真命題,q是假命題,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分16分)已知![]() 為實數,函數
為實數,函數![]() ,函數
,函數![]() .
.
(1)當![]() 時,令
時,令![]() ,求函數
,求函數![]() 的極值;
的極值;
(2)當![]() 時,令
時,令![]() ,是否存在實數
,是否存在實數![]() ,使得對于函數
,使得對于函數![]() 定義域中的任意實數
定義域中的任意實數![]() ,均存在實數
,均存在實數![]() ,有
,有![]() 成立,若存在,求出實數
成立,若存在,求出實數![]() 的取值集合;若不存在,請說明理由.
的取值集合;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費用支出x萬元與銷售額y萬元之間有如下的對應數據:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)畫出散點圖;
(2)求回歸直線方程;
(3)據此估計廣告費用為12萬元時,銷售收入y的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分16分)
在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
: ![]() 的離心率
的離心率![]() ,直線
,直線![]() 過橢圓
過橢圓![]() 的右焦點
的右焦點![]() ,且交橢圓
,且交橢圓![]() 于
于![]() ,
, ![]() 兩點.
兩點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知點![]() ,連結
,連結![]() ,過點
,過點![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() ,設直線
,設直線![]() 與直線
與直線![]() 交于點
交于點![]() ,試探索當
,試探索當![]() 變化時,是否存在一條定直線
變化時,是否存在一條定直線![]() ,使得點
,使得點![]() 恒在直線
恒在直線![]() 上?若存在,請求出直線
上?若存在,請求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某學校一名籃球運動員在五場比賽中所得分數的莖葉圖,則該運動員在這五場比賽中得分的方差為 .
(注:方差 ![]() ,其中
,其中 ![]() 為x1 , x2 , …,xn的平均數)
為x1 , x2 , …,xn的平均數)![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分10分)如圖,在長方體![]() 中,
中,![]() ,
,![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,點
,點![]() 在線段
在線段![]() 上(點
上(點![]() 與點
與點![]() 不重合).
不重合).

(1)若異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() ,求
,求![]() 的長度;
的長度;
(2)若![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】射擊測試有兩種方案,方案1:先在甲靶射擊一次,以后都在乙靶射擊;方案2:始終在乙靶射擊,某射手命中甲靶的概率為![]() ,命中一次得3分;命中乙靶的概率為
,命中一次得3分;命中乙靶的概率為![]() ,命中一次得2分,若沒有命中則得0分,用隨機變量
,命中一次得2分,若沒有命中則得0分,用隨機變量![]() 表示該射手一次測試累計得分,如果
表示該射手一次測試累計得分,如果![]() 的值不低于3分就認為通過測試,立即停止射擊;否則繼續射擊,但一次測試最多打靶3次,每次射擊的結果相互獨立。
的值不低于3分就認為通過測試,立即停止射擊;否則繼續射擊,但一次測試最多打靶3次,每次射擊的結果相互獨立。
(1)如果該射手選擇方案1,求其測試結束后所得分![]() 的分布列和數學期望E
的分布列和數學期望E![]() ;
;
(2)該射手選擇哪種方案通過測試的可能性大?請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com