
【題目】P(x0 , y0)(x0≠±a)是雙曲線E: ![]() 上一點,M,N分別是雙曲線E的左右頂點,直線PM,PN的斜率之積為
上一點,M,N分別是雙曲線E的左右頂點,直線PM,PN的斜率之積為 ![]() .
.
(1)求雙曲線的離心率;
(2)過雙曲線E的右焦點且斜率為1的直線交雙曲線于A,B兩點,O為坐標原點,C為雙曲線上一點,滿足 ![]() ,求λ的值.
,求λ的值.
【答案】
(1)解:∵P(x0,y0)(x0≠±a)是雙曲線E: ![]() 上一點,
上一點,
∴ ![]() ,①
,①
由題意又有 ![]() ,②
,②
聯立①、②可得a2=5b2,c2=a2+b2,
則e= ![]() ,
,
(2)聯立 ![]() ,得4x2﹣10cx+35b2=0,
,得4x2﹣10cx+35b2=0,
設A(x1,y1),B(x2,y2),
則x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
設 ![]() =(x3,y3),
=(x3,y3), ![]() ,
,
即 ![]()
又C為雙曲線上一點,即x32﹣5y32=5b2,
有(λx1+x2)2﹣5(λy1+y2)2=5b2,
化簡得:λ2(x12﹣5y12)+(x22﹣5y22)+2λ(x1x2﹣5y1y2)=5b2,
又A(x1,y1),B(x2,y2)在雙曲線上,所以x12﹣5y12=5b2,x22﹣5y22=5b2,
而x1x2﹣5y1y2=x1x2﹣5(x1﹣c)(x2﹣c)
=﹣4x1x2+5c(x1+x2)﹣5c2=﹣4 ![]() +5c
+5c ![]() ﹣5c2=
﹣5c2= ![]() ﹣35b2=
﹣35b2= ![]() 6b2﹣35b2=10b2,
6b2﹣35b2=10b2,
得λ2+4λ=0,解得λ=0或﹣4.
【解析】(1)由P點坐標滿足雙曲線方程,直線PM,PN的斜率之積為 ![]() 聯立方程組可得a2=5b2,即可求出e的值。
聯立方程組可得a2=5b2,即可求出e的值。
(2)可求出過雙曲線E的右焦點且斜率為1的直線y=x-c,與雙曲線聯立方程組求出x1+x2,x1x2。由 ![]() 可求出
可求出![]() 值。
值。


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩人參加普法知識競賽,共有5個不同題目,選擇題3個,判斷題2個,甲、乙兩人各抽一題.
(1)求甲抽到判斷題,乙抽到選擇題的概率是多少;
(2)求甲、乙兩人中至少有一人抽到選擇題的概率是多少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0,函數f(x)=ax2+bx+c,若x0滿足關于x的方程2ax+b=0,則下列選項的命題中為假命題的是( )
A.x∈R,f(x)≤f(x0)
B.x∈R,f(x)≥f(x0)
C.x∈R,f(x)≤f(x0)
D.x∈R,f(x)≥f(x0)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓 ![]() =1(a>b>0),F1 , F2分別為橢圓的左、右焦點,A為橢圓的上頂點,直線AF2交橢圓于另一點B.
=1(a>b>0),F1 , F2分別為橢圓的左、右焦點,A為橢圓的上頂點,直線AF2交橢圓于另一點B.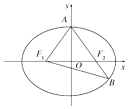
(1)若∠F1AB=90°,求橢圓的離心率;
(2)若橢圓的焦距為2,且 ![]() =2
=2 ![]() ,求橢圓的方程.
,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題:其中正確命題的序號是 .
①設a,b是非零實數,若a<b,則ab2<a2b;
②若a<b<0,則 ![]() >
> ![]() ;
;
③函數y= ![]() 的最小值是2;
的最小值是2;
④若x,y是正數, ![]() +
+ ![]() =1,則x+2y的最小值為8.
=1,則x+2y的最小值為8.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列結論正確的個數是( )
①若正實數![]() 滿足
滿足![]() ,則
,則![]() 的最小值是16;
的最小值是16;
②已知![]() ,則函數
,則函數![]() 的最大值為
的最大值為![]() ;
;
③已知![]() ,且
,且![]() ,則
,則![]() 的最小值是36;
的最小值是36;
④若對任意實數![]() ,不等式
,不等式![]() 恒成立,則實數
恒成立,則實數![]() 的取值范圍是
的取值范圍是![]() 。
。
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com