【題目】如圖，在邊長為25cm的正方形中挖去邊長為23cm的兩個等腰直角三角形，現有均勻的粒子散落在正方形中，問粒子落在中間帶形區域的概率是多少？
【答案】答：因為均勻的粒子落在正方形內任何一點是等可能的
所以符合幾何概型的條件。
設A＝“粒子落在中間帶形區域”則依題意得
正方形面積為：25×25＝625
兩個等腰直角三角形的面積為：2×
×23×23＝529
帶形區域的面積為：625－529＝96
∴ P（A）＝
【解析】
求出帶形區域的面積，并求出正方形面積用來表示全部基本事件，再由幾何概型公式，即可求解．
因為均勻的粒子落在正方形內任何一點是等可能的
所以符合幾何概型的條件．
設A＝“粒子落在中間帶形區域”則依題意得
正方形面積為：25×25＝625
兩個等腰直角三角形的面積為：2×
×23×23＝529
帶形區域的面積為：625﹣529＝96
∴P（A）＝
，
則粒子落在中間帶形區域的概率是．
故答案為：．
科目：高中數學 來源： 題型：
【題目】現有4個人去參加某娛樂活動，該活動有甲、乙兩個游戲可供參加者選擇．為增加趣味性，約定：每個人通過擲一枚質地均勻的骰子決定自己去參加哪個游戲，擲出點數為1或2的人去參加甲游戲，擲出點數大于2的人去參加乙游戲．
(1)求這4個人中恰有2個人去參加甲游戲的概率；
(2) 用X表示這4個人中去參加乙游戲的人數，求隨機變量X的分布列與數學期望E（X）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線
是極坐標方程式
，以極點為平面直角坐標系的原點，極軸為
軸的正半軸，建立平面直角坐標系，直線
是參數方程是
（
為參數）.
（1）求曲線
的直角坐標方程和直線
的普通方程；
（2）設點
，若直線
與曲線
交于兩點
，且
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某商場購進一種每件價格為90元的新商品，在商場試銷時發現：銷售單價
（元/件）與每天銷售量
（件）之間滿足如圖所示的關系．
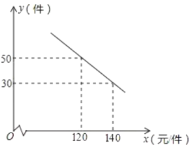
（1）求出與之間的函數關系式；
（2）寫出每天的利潤
與銷售單價之間的函數關系式，并求出售價定為多少時，每天獲得的利潤最大？最大利潤是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知二次函數
的圖像與
軸相交于點
、
（點在點的左側），與
軸相交于點
，連接
、
．
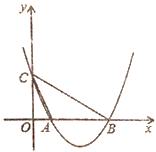
（1）求線段
的長；
（2）若平分
，求
的值；
（3）該函數圖象的對稱軸上是否存在點
，使得
為等邊三角形？若存在，求出的值；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“干支紀年法”是中國歷法上自古以來使用的紀年方法，甲、乙、丙、丁、戊、己、庚、辛、壬、癸被稱為“十天干”，子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字開始，“地支”以“子”字開始，兩者按干支順序相配，組成了干支紀年法，其相配順序為：甲子、乙丑、丙寅…癸酉，甲戌、乙亥、丙子…癸末，甲申、乙酉、丙戌…癸巳，…，共得到
個組成，周而復始，循環記錄。2014年是“干支紀年法”中的甲午年，那么2020年是“干支紀年法”中的（）
A. 己亥年 B. 戊戌年 C. 辛丑年 D. 庚子年
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
