【題目】已知函數 
．
（I） 討論函數
的單調區間；
（II）當
時，若函數
在區間
上的最大值為3，求
的取值范圍．
【答案】（Ⅰ）當
時， 
在
內單調遞增， 
在
內單調遞減；當
時， 
在
單調遞增；當
時， 
在
內單調遞增， 
在
內單調遞減；（Ⅱ）即
的取值范圍是
．
【解析】試題分析：（I）求導，求出導數的零點，討論
與
的大小與導數的符號寫出單調區間即可；（II）當
時寫出函數的單調區間，確定函數極大值與極小值，可知
.
試題解析：（I）
． 1分
令
得
． 2分
（i）當
，即
時， 
， 
在
單調遞增． 3分
（ii）當
，即
時，
當
時
， 
在
內單調遞增；
當
時
， 
在
內單調遞減． 4分
（iii）當
，即
時，
當
時
， 
在
內單調遞增；
當
時
， 
在
內單調遞減． 5分
綜上，當
時， 
在
內單調遞增， 
在
內單調遞減；
當
時， 
在
單調遞增；
當
時， 
在
內單調遞增，
在
內單調遞減．（其中
） 6分
（II）當
時， 
， 
令
，得
． 7分
將
， 
， 
變化情況列表如下：
|
|
|
| 1 |
|
|
| 0 |
| 0 |
|
| ↗ | 極大 | ↘ | 極小 | ↗ |
8分
由此表可得
， 
． 9分
又
， 10分
故區間
內必須含有
，即
的取值范圍是
． 12分
學而優暑期銜接南京大學出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目：高中數學 來源： 題型：
【題目】如圖所示的鋼板的邊界
是拋物線的一部分，且
垂直于拋物線對稱軸，現欲從鋼板上截取一塊以
為下底邊的等腰梯形鋼板
，其中
均在拋物線弧上.設
（米），且
.
（1）當
時，求等腰梯形鋼板的面積;
（2）當
為何值時，等腰梯形鋼板的面積最大？并求出最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如果集合A，B，同時滿足A∪B={1，2，3，4}，A∩B={1}，A≠{1}，B≠{1}，就稱有序集對（A，B）為“好集對”．這里有序集對（A，B）意指，當A≠B時，（A，B）和（B，A）是不同的集對，那么“好集對”一共有（ ）個．
A.5
B.6
C.7
D.8
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于任意實數x，[x]表示不超過x的最大整數，如[1.1]=1，[﹣2.1]=﹣3．定義在R上的函數f（x）=[2x]+[4x]+[8x]，若A={y|y=f（x），0＜x＜1}，則A中所有元素之和為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一企業從某條生產線上隨機抽取30件產品，測量這些產品的某項技術指標值
,得到如下的頻數分布表:
|
|
|
|
|
頻數 | 2 | 6 | 18 | 4 |
(I)估計該技術指標值的平均數；（用各組區間中點值作代表）
(II) 若
或
，則該產品不合格，其余的是合格產品，試估計該條生產線生產的產品為合格品的概率；
(III)生產一件產品,若是合格品可盈利80元,不合格品則虧損10元,在(II)的前提下,從該生產線生產的產品中任取出兩件，記
為兩件產品的總利潤,求隨機變量X的分布列和期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
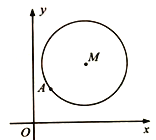
【題目】如圖，在平面直角坐標系
中，已知以
為圓心的圓
及其上一點
.
（1）設圓
與
軸相切，與圓
外切，且圓心
在直線
上，求圓
的標準方程；
（2）設平行于
的直線
與圓
相交于
兩點，且
,求直線
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
