【題目】已知
．
（Ⅰ）若函數
在
上單調遞增，求實數
的取值范圍；
（Ⅱ）若
，證明：
，
恒成立．
【答案】見解析
【解析】（Ⅰ）
．
由函數
在
上單調遞增，可得
在上恒成立，
即
，得
． -----------------2分
記
（
），則
．
當
時，
，函數單調遞減；當
時，
，函數單調遞增．
所以
． -----------------5分
所以實數
的取值范圍為
． ---------------------------6分
（Ⅱ）設
．
則
，
記
，則
，
故當
時，
，函數
單調遞減；
當
時，
，函數單調遞增． ------------9分
又
，
，所以
，使得
，即
．
所以當
時，
，函數單調遞增；
當
時，
，函數單調遞減；
當
時，，函數單調遞增．
而
，
所以
時，
，即
恒成立． -----------------13分
【命題意圖】本題考查導數與函數的單調性、不等式的證明等，考查基本的邏輯推理能力、運算能力以及數學應用意識等．
每課必練系列答案
巧學巧練系列答案科目：高中數學 來源： 題型：
【題目】函數f（x）＝xlnx－a（x－1）2－x，g（x）＝lnx－2a（x－1），其中常數a∈R．
（Ⅰ）討論g（x）的單調性；
（Ⅱ）當a＞0時，若f（x）有兩個零點x1，x2（x1＜x2），求證：在區間（1，＋∞）上存在f（x）的極值點x0，使得x0lnx0＋lnx0－2x0＞0．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某廠生產某種產品x（百臺），總成本為C（x）（萬元），其中固定成本為2萬元，每生產1百臺，成本增加1萬元，銷售收入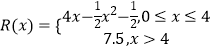 
（萬元），假定該產品產銷平衡．
（1）若要該廠不虧本，產量x應控制在什么范圍內？
（2）該廠年產多少臺時，可使利潤最大？
（3）求該廠利潤最大時產品的售價．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司生產一種產品，第一年投入資金1000萬元，出售產品收入40萬元，預計以后每年的投入資金是上一年的一半，出售產品所得收入比上一年多80萬元，同時，當預計投入的資金低于20萬元時，就按20萬元投入，且當年出售產品收入與上一年相等.
（1）求第
年的預計投入資金與出售產品的收入；
（2）預計從哪一年起該公司開始盈利？（注：盈利是指總收入大于總投入）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
