
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,拋物線
,拋物線![]() 與橢圓
與橢圓![]() 有相同的焦點,且橢圓
有相同的焦點,且橢圓![]() 過點
過點![]() .
.
(I)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若橢圓![]() 的右頂點為
的右頂點為![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點(
兩點(![]() 與
與![]() 點不重合),且滿足
點不重合),且滿足![]() ,若點
,若點![]() 為
為![]() 中點,求直線
中點,求直線![]() 斜率的最大值.
斜率的最大值.

【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】試題分析:
(Ⅰ)寫出拋物線焦點坐標,得橢圓中![]() ,把點
,把點![]() 的坐標代入橢圓方程得
的坐標代入橢圓方程得![]() 與
與![]() 聯立可解得
聯立可解得![]() ,得橢圓方程;
,得橢圓方程;
(Ⅱ)設![]() ,設直線方程為
,設直線方程為![]() ,與橢圓方程聯立消元后應用教研室可得
,與橢圓方程聯立消元后應用教研室可得![]() ,
,![]() ,用
,用![]() 代
代![]() 可得F點坐標,計算中點P坐標,計算AP的斜率為
可得F點坐標,計算中點P坐標,計算AP的斜率為![]() ,分子分母同時除以
,分子分母同時除以![]() ,并換元
,并換元![]() ,得
,得![]() ,由基本不等式可得最大值.
,由基本不等式可得最大值.
試題解析:
(Ⅰ)因為拋物線![]() 的焦點為
的焦點為![]() ,拋物線與橢圓C有相同的焦點
,拋物線與橢圓C有相同的焦點
所以![]() ,又橢圓
,又橢圓![]() 過點
過點![]() ,所以
,所以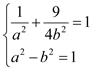 解得
解得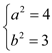 .
.
則橢圓的標準方程為![]() ;
;
(Ⅱ)設![]() ,
,![]()
直線AE的方程為![]() ,代入橢圓方程,可得
,代入橢圓方程,可得![]()
由![]() ,可得
,可得![]() ,
,![]() ,
,
由于AE⊥AF,只要將上式的![]() 換為
換為![]() ,可得
,可得![]() ,
,![]() ,
,
由P為EF的中點,得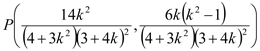
則直線AP的斜率為![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,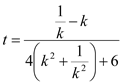 ,
,
再令![]() ,可得
,可得![]() ,當
,當![]() 時,
時,![]() ;
;
當![]() 時,
時,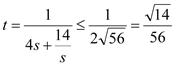 ,
,
當且僅當![]() 時,取得最大值;
時,取得最大值;
綜上可得直線AP的斜率的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知A、B、C是△ABC的三個內角,則在下列各結論中,不正確的為( )
A. sin2A=sin2B+sin2C+2sinBsinCcos(B+C)
B. sin2B=sin2A+sin2C+2sinAsinCcos(A+C)
C. sin2C=sin2A+sin2B-2sinAsinBcosC
D. sin2(A+B)=sin2A+sin2B-2sinBsinCcos(A+B)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,若存在
,若存在![]() ,滿足
,滿足![]() ,則稱
,則稱![]() 是
是![]() 的一個“友好”三角形.
的一個“友好”三角形.
(ⅰ)在滿足下述條件的三角形中,存在“友好”三角形的是__________;(請寫出符合要求的條件的序號).
①![]() ,
,![]() ,
,![]() ; ②
; ②![]() ,
,![]() ,
,![]() ;
;
③![]() ,
,![]() ,
,![]() .
.
(ⅱ)若![]() 存在“友好”三角形,且
存在“友好”三角形,且![]() ,在另外兩個角的度數分別為__________.
,在另外兩個角的度數分別為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校100名學生期中考試數學成績的頻率分布直方圖如圖:
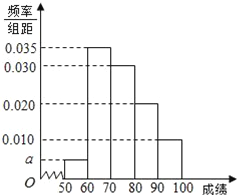
(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生期中考試數學成績的平均分;
(3)現用分層抽樣的方法從第3、4、5組中隨機抽取6名學生,將該樣本看成一個總體,從中隨機抽取2名,求其中恰有1人的分數不低于90分的概率?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙二人用4張撲克牌(分別是紅桃2,紅桃3,紅桃4,方片4)完游戲,他們將撲克牌洗勻后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一張.
(1)設![]() 分別表示甲、乙抽到的牌的數字,寫出甲乙二人抽到的牌的所有情況;
分別表示甲、乙抽到的牌的數字,寫出甲乙二人抽到的牌的所有情況;
(2)若甲抽到紅桃3,則乙抽出的牌的牌面數字比3大的概率是多少?
(3)甲乙約定:若甲抽到的牌的牌面數字比乙大,則甲勝,反之,則乙勝,你認為此游戲是否公平,說明你的理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設 ![]() ,
, ![]() ,
, ![]() 均為非零向量,已知命題p:
均為非零向量,已知命題p: ![]() =
= ![]() 是
是 ![]()
![]() =
= ![]()
![]() 的必要不充分條件,命題q:x>1是|x|>1成立的充分不必要條件,則下列命題是真命題的是( )
的必要不充分條件,命題q:x>1是|x|>1成立的充分不必要條件,則下列命題是真命題的是( )
A.p∧q
B.p∨q
C.(¬p)∧(¬q)
D.p∨(¬q)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com