【題目】已知
，
是兩條不同直線，
，
是兩個不同平面，則下列命題正確的是（ ）
A.若，垂直于同一平面，則與平行
B.若，平行于同一平面，則與平行
C.若，不平行，則在內不存在與平行的直線
D.若，不平行，則與不可能垂直于同一平面
科目：高中數學 來源： 題型：
【題目】選修4—4：坐標系與參數方程。
在平面直角坐標系xOy中，已知曲線
，以平面直角坐標系xOy的原點O為極點，x軸的正半軸為極軸，取相同的單位長度建立極坐標系，已知直線
．
（1）將曲線
上的所有點的橫坐標、縱坐標分別伸長為原來的
、2倍后得到曲線
，試寫出直線
的直角坐標方程和曲線的參數方程；
（2）在曲線上求一點P，使點P到直線
的距離最大，并求出此最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面內有兩個定點A（1，0），B（1，﹣2），設點P到A、B的距離分別為
，且
（I）求點P的軌跡C的方程；
（II）是否存在過點A的直線
與軌跡C相交于E、F兩點，滿足
（O為坐標原點）．若存在，求出直線的方程；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項為和Sn，點（n，
）在直線y＝
x＋
上．數列{bn}滿足bn+2－2bn+1＋bn＝0（nN*），且b3＝11，前9項和為153．
（1）求數列{an}，{bn}的通項公式；
（2）求數列
的前
項和
（3）設nN*，f（n）＝
問是否存在mN*，使得f（m＋15）＝5f（m）成立？若存在，求出m的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列變化過程中，變量之間不是函數關系的為（ ）
A.地球繞太陽公轉的過程中，二者間的距離與時間的關系
B.在銀行，給定本金和利率后，活期存款的利息與存款天數的關系
C.某地區玉米的畝產量與灌溉次數的關系
D.近年來中國高鐵年運營里程與年份的關系
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在發生某公共衛生事件期間，有專業機構認為該事件在一段時間沒有發生在規模群體感染的標志為“連續10天，每天新增疑似病例不超過7人”。根據過去10天甲、乙、丙、丁四地新增疑似病例數據，一定符合該標志的是 （ ）
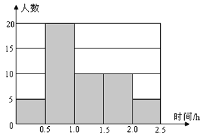
A. 甲地：總體均值為3，中位數為4
B. 乙地：總體均值為1，總體方差大于0
C. 丙地：中位數為2，眾數為3
D. 丁地：總體均值為2，總體方差為3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一盒中裝有除顏色外其余均相同的12個小球，從中隨機取出1個球，取出紅球的概率為
，取出黑球的概率為
，取出白球的概率為
，取出綠球的概率為
.求：
（1）取出的1個球是紅球或黑球的概率；
（2）取出的1個球是紅球或黑球或白球的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的兩個焦點為
，
，離心率為
，點
，
在橢圓上，在線段
上，且
的周長等于
．
（1）求橢圓
的標準方程；
（2）過圓
上任意一點
作橢圓
的兩條切線
和
與圓
交于點
，
，求
面積的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
