Question

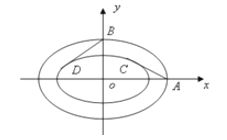
【題目】某奧運會主體育場的簡化鋼結(jié)構(gòu)俯視圖如圖所示，內(nèi)外兩圈的鋼骨架是離心率相同的橢圓，我們稱這兩個橢圓相似。

（1）已知橢圓，寫出與橢圓相似且焦點在軸上、短半軸長為的橢圓的標準方程；若在橢圓上存在兩點、關(guān)于直線對稱，求實數(shù)的取值范圍；

（2）從外層橢圓頂點A、B向內(nèi)層橢圓引切線AC、BD，設(shè)內(nèi)層橢圓方程為+=1 (ab0)，AC與BD的斜率之積為－，求橢圓的離心率。

Answer 1

【答案】（1）；（2）．

【解析】試題分析：

（1）由兩點、關(guān)于直線對稱可設(shè)出直線的方程為，將此方程與橢圓方程聯(lián)立消去y可得，由題意此方程有兩個不等實根，再根據(jù)的中點在直線上可消去t，根據(jù)判別式可得的范圍；

（2）設(shè)外層的橢圓的方程為，切線的方程為，由直線與橢圓相切根據(jù)判別式為零可得，同理切線BD的斜率，故，結(jié)合條件可得，根據(jù)此結(jié)論可求得。

試題解析：

（1）橢圓的方程為：

設(shè)直線的方程為，

由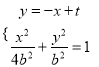消去y整理得

設(shè)點， 中點為，

則

所以

因為中點在直線上，

所以，

解得

所以直線的方程為，

由題意可知，直線與橢圓有兩個不同的交點，

即方程有兩個不同的實數(shù)解，

所以，

解得或（舍去）。

所以實數(shù)的取值范圍為。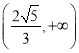

（2）設(shè)外層的橢圓的方程為，

設(shè)切線的方程為,

由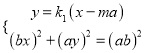消去y整理得

∵直線與橢圓相切，

∴，

整理得,

同理

∴，∴，

由題意得

∴，∴。

即橢圓的離心率為。